题目内容
17.若cosθ=$\frac{2}{3}$,θ为第四象限角,则cos(θ+$\frac{π}{4}$)的值为( )| A. | $\frac{\sqrt{2}+\sqrt{10}}{6}$ | B. | $\frac{2\sqrt{2}+\sqrt{10}}{6}$ | C. | $\frac{\sqrt{2}-\sqrt{10}}{6}$ | D. | $\frac{2\sqrt{2}-\sqrt{10}}{6}$ |
分析 可先由同角三角函数的基本关系求出θ的正弦,然后由余弦的和角公式求出的值即可得到答案
解答 解:cosθ=$\frac{2}{3}$,θ为第四象限角,得sinθ=-$\sqrt{1-\frac{4}{9}}$=-$\frac{\sqrt{5}}{3}$,
∴cos(θ+$\frac{π}{4}$)=cosθcos$\frac{π}{4}$-sinθsin$\frac{π}{4}$=$\frac{2}{3}$×$\frac{\sqrt{2}}{2}$+$\frac{\sqrt{5}}{3}$×$\frac{\sqrt{2}}{2}$=$\frac{2\sqrt{2}+\sqrt{10}}{6}$.
故选:B
点评 本题考点是三角函数的恒等变换及化简求值,考查了同角三角函数的基本关系,余弦的和角公式,解题的关键是熟练掌握三角函数的公式,利用公式求值,三角函数公式较多,变形灵活,做题时要注意总结规律,找到最佳的变形方法进行求值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.三棱锥P-ABC中,AB=AC=PB=PC=5,PA=BC若该三棱锥的四个顶点在同一个球面上,且球的表面积为34π,则棱PA的长为( )
| A. | 3 | B. | $2\sqrt{3}$ | C. | $3\sqrt{2}$ | D. | 5 |
8.根据如下的样本数据:
得到的回归方程为y=bx+a,其中b为9.4,据此模型预报广告费为6万元时的销售额为( )
| 广告费x/万元 | 4 | 2 | 3 | 5 |
| 销售额y/万元 | 49 | 26 | 39 | 54 |
| A. | 63.6万元 | B. | 65.5万元 | C. | 67.7万元 | D. | 72.0万元 |
5.欧阳修在《卖油翁》中写到:“(翁)乃取一葫芦置于地,以钱覆其口,徐以杓酌油沥之,自钱孔入,而钱不湿”,可见卖油翁的技艺之高超,若铜钱直径为20mm,中间有边长为5mm的正方形小孔,随机向铜钱上滴一滴油(油滴大小忽略不计),则油恰好落入孔中的概率是( )
| A. | $\frac{1}{4π}$ | B. | $\frac{1}{2π}$ | C. | $\frac{1}{π}$ | D. | $\frac{2}{π}$ |
2.随着互联网经济逐步被人们接受,网上购物的人群越来越多,网上交易额也逐年增加,某地一建设银行连续五年的网银交易额统计表,如表所示:
经研究发现,年份与网银交易额之间呈线性相关关系,为了计算的方便,工作人员将上表的数据进行了处理,t=x-2011,z=y-5,得到如表:
(1)求z关于t的线性回归方程;
(2)通过(1)中的方程,求出y关于x的回归方程;
(3)用所求回归方程预测到2020年年底,该地网银交易额可达多少?
(附:在线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$中,$b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2}-n{{(\overline x)}^2}}}=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y})}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}$,$a=\overline y-b\overline x$)
| 年份x | 2012 | 2013 | 2014 | 2015 | 2016 |
| 网上交易额y(亿元) | 5 | 6 | 7 | 8 | 10 |
| 时间代号t | 1 | 2 | 3 | 4 | 5 |
| z | 0 | 1 | 2 | 3 | 5 |
(2)通过(1)中的方程,求出y关于x的回归方程;
(3)用所求回归方程预测到2020年年底,该地网银交易额可达多少?
(附:在线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$中,$b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2}-n{{(\overline x)}^2}}}=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y})}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}$,$a=\overline y-b\overline x$)
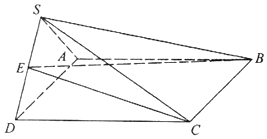 如图,四棱锥S-ABCD中,底面ABCD是边长为4的正方形,平面SAD⊥平面SCD,$SA=SD=2\sqrt{2}$.
如图,四棱锥S-ABCD中,底面ABCD是边长为4的正方形,平面SAD⊥平面SCD,$SA=SD=2\sqrt{2}$.