题目内容
15.已知数列{an}为等差数列,{bn}为等比数列,且an>0,bn>0,记数列{an•bn}的前n项和为Sn,若a1=b1=1,Sn=(n-1)•3n+1(n∈N*),则数列{$\frac{{a}_{n}-25}{{b}_{n}}$}的最大项为第14项.分析 设等差数列{an}的公差为d(d>0),等比数列{bn}的公比为q(q>0),由已知列式求得公差和公比,得到等差数列与等比数列的通项公式,代入$\frac{{a}_{n}-25}{{b}_{n}}$,化简整理,令cn=$\frac{{a}_{n}-25}{{b}_{n}}$,由$\left\{\begin{array}{l}{{c}_{n}≥{c}_{n-1}}\\{{c}_{n}≥{c}_{n+1}}\end{array}\right.$ 求得n值.
解答 解:设等差数列{an}的公差为d(d>0),等比数列{bn}的公比为q(q>0),
由Sn=(n-1)•3n+1,得
$\left\{\begin{array}{l}{{S}_{2}=1+(1+d)q=10}\\{{S}_{3}=1+(1+d)q+(1+2d){q}^{2}=55}\end{array}\right.$,
即$\left\{\begin{array}{l}{(1+d)q=9}\\{(1+2d){q}^{2}=45}\end{array}\right.$,解得d=2,q=3.
∴an=1+2(n-1)=2n-1,${b}_{n}={3}^{n-1}$.
∴$\frac{{a}_{n}-25}{{b}_{n}}$=$\frac{2n-26}{{3}^{n-1}}$,
令${c}_{n}=\frac{2n-26}{{3}^{n-1}}$,由$\left\{\begin{array}{l}{{c}_{n}≥{c}_{n-1}}\\{{c}_{n}≥{c}_{n+1}}\end{array}\right.$,
得$\left\{\begin{array}{l}{\frac{2n-26}{{3}^{n-1}}≥\frac{2n-28}{{3}^{n-2}}①}\\{\frac{2n-26}{{3}^{n-1}}≥\frac{2n-24}{{3}^{n}}②}\end{array}\right.$,
由①得$n≤\frac{29}{2}$,由②得n$≥\frac{27}{2}$.
∴n=14.
即数列{$\frac{{a}_{n}-25}{{b}_{n}}$}的最大项为第14项.
故答案为:14.
点评 本题是等差数列与等比数列的综合题,考查了等差数列与等比数列的通项公式,考查数列的函数特性,是中档题.

| A. | ($\frac{1}{4}$,1) | B. | ($\frac{3}{4}$,$\frac{3}{2}$) | C. | ($\frac{1}{4}$,$\frac{5}{4}$) | D. | ($\frac{5}{4}$,2) |
| A. | a | B. | 2a | C. | 2$\sqrt{1-a}$-4 | D. | 2$\sqrt{2-a}$-4 |
| A. | 试验组的对象必须是随机选取的 | |
| B. | 必须有试验组和对照组 | |
| C. | 对照组中的对象不必使用安慰剂 | |
| D. | 在有些随机对照试验中,为了得到更真实的结果,有时还需要使用安慰剂 |
| A. | 40$\sqrt{3}$ | B. | $\frac{80\sqrt{3}}{3}$ | C. | 40$\sqrt{2}$ | D. | $\frac{80\sqrt{2}}{3}$ |
| A. | 证明n=0时,n2<2n | B. | 证明n=5时,n2<2n | C. | 证明n=1时,n2<2n | D. | 证明n=6时,n2<2n |
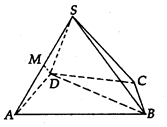 如图,四棱锥S-ABCD中,△ABD是正三角形,CB=CD,SC⊥BD.
如图,四棱锥S-ABCD中,△ABD是正三角形,CB=CD,SC⊥BD.