题目内容
13.圆x2+y2=4与圆x2+y2-10x+16=0的位置关系为( )| A. | 相交 | B. | 外切 | C. | 内切 | D. | 外离 |
分析 把第二个圆的方程化为标准方程,找出圆心A的坐标和半径r,再由第一个圆的方程找出圆心B的坐标和半径R,利用两点间的距离公式求出两圆心间的距离d,发现d=R+r,从而判断出两圆位置关系是外切.
解答 解:把圆x2+y2-10x+16=0化为标准方程得:(x-5)2+y2=9,
∴圆心A的坐标为(5,0),半径r=3,
由圆x2+y2=4,得到圆心B坐标为(0,0),半径R=2,
两圆心间的距离d=|AB|=5,
∵2+3=5,即d=R+r,
则两圆的位置关系是外切.
故选:B.
点评 此题考查了圆的标准方程,两点间的距离公式,以及圆与圆位置关系的判断,圆与圆位置关系的判断方法为:当0≤d<R-r时,两圆内含;当d=R-r时,两圆内切;当R-r<d<R+r时,两圆相交;当d=R+r时,两圆外切;当d>R+r时,两圆相离(d表示两圆心间的距离,R及r分别表示两圆的半径).

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
4.设复数z满足(1+i)z=|1+i|,则复数z在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
8.一次考试中,要求考生从试卷上的9个题目中选6个进行答题,则考生不同的选择答题的种数为( )
| A. | 6 | B. | 84 | C. | 504 | D. | 69 |
2.已知集合A={x|x2-2x-3≤0},B={x|4x≥2},则A∪B=( )
| A. | $[{\frac{1}{2},3}]$ | B. | $[{\frac{1}{2},3})$ | C. | (-∞,3] | D. | [-1,+∞) |
3.已知f(x)=acos(x+2θ)+bx+3(a,b为非零常数),若f(1)=5,f(-1)=1,则θ的可能取值为( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{6}$ |

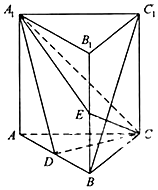 如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=$\frac{{\sqrt{2}}}{2}$AB.
如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=$\frac{{\sqrt{2}}}{2}$AB.