题目内容
4.设复数z满足(1+i)z=|1+i|,则复数z在复平面内对应的点位于( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 把已知的等式变形,然后利用复数代数形式的乘除运算化简,求得z所对应点的坐标得答案.
解答 解:$z=\frac{{|{1+i}|}}{1+i}=\frac{{\sqrt{2}}}{2}-\frac{{\sqrt{2}}}{2}i$,故复数z所对应的点为$({\frac{{\sqrt{2}}}{2},-\frac{{\sqrt{2}}}{2}})$在第四象限.
故选D.
点评 本题考查复数代数形式的乘除运算,考查复数的代数表示法及其几何意义,是基础题.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
19.已知等差数列{an}的公差d不为零,前n项和是Sn,若a3,a5,a10成等比数列,则( )
| A. | a1d>0,dS4>0 | B. | a1d>0,dS4<0 | C. | a1d<0,dS4>0 | D. | a1d<0,dS4<0 |
13.圆x2+y2=4与圆x2+y2-10x+16=0的位置关系为( )
| A. | 相交 | B. | 外切 | C. | 内切 | D. | 外离 |
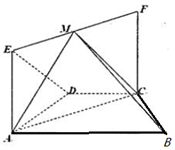 如图,在等腰梯形ABCD中,AB∥CD,AD=DC=CB=2,∠ABC=60°,四边形ACFE为矩形,CF=$\sqrt{3}$,平面ACFE⊥平面ABCD,点M为线段EF中点.
如图,在等腰梯形ABCD中,AB∥CD,AD=DC=CB=2,∠ABC=60°,四边形ACFE为矩形,CF=$\sqrt{3}$,平面ACFE⊥平面ABCD,点M为线段EF中点.