题目内容
18.已知AB是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴,若把该长轴2010等分,过每个等分点作AB的垂线,依次交椭圆的上半部分于点P1,P2,…,P2009,设左焦点为F1,则$\frac{1}{2010}$(|F1A|+|F1P1|+|F1P2|+…+|F1P2009|+|F1B|)=$\frac{2011}{2010}a$.分析 设右焦点为F2,由椭圆的定义可得|F1Pi|+|F2Pi|=2a,(1≤i≤2009,i∈N),点P1,P2,…,Pn-1 关于y轴成对称分布,|F1Pi|+|F1P2010-i|=2a,|F1P1005|=a,|F1A|+|F1B|=2a,即可求得|F1A|+|F1P1|+|F1P2|+…+|F1P2009|+|F1B|的值,求得$\frac{1}{2010}$(|F1A|+|F1P1|+|F1P2|+…+|F1P2009|+|F1B|)=$\frac{2011}{2010}a$.
解答 解:设右焦点为F2,由椭圆的定义可得|F1Pi|+|F2Pi|=2a,(1≤i≤2009,i∈N),
由题意知点P1,P2,…,Pn-1 关于y轴成对称分布,
∴|F1Pi|+|F1P2010-i|=2a,|F1P1005|=a,|F1A|+|F1B|=2a,
|F1A|+|F1P1|+|F1P2|+…+|F1P2009|+|F1B|=2a×1004+2a+a=2011a,
$\frac{1}{2010}$(|F1A|+|F1P1|+|F1P2|+…+|F1P2009|+|F1B|)=$\frac{2011}{2010}a$,
故答案为:$\frac{2011}{2010}a$.
点评 本题考查椭圆的定义,考查椭圆的简单几何性质,考查计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.若一个正三棱锥的正(主)视图如图所示,则其体积等于( )
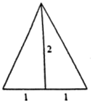

| A. | $\frac{{\sqrt{3}}}{6}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{2\sqrt{3}}}{3}$ | D. | $2\sqrt{3}$ |
6.在对人们的休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人,女性中有43人主要的休闲方式是看电视,其余人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,其余人主要的休闲方式是运动.
(1)根据以上数据建立一个2×2的列联表;
(2)能否在犯错误的概率不超过0.01的前提下,认为休闲方式与性别有关系.
参考临界值表
(1)根据以上数据建立一个2×2的列联表;
| 看电视 | 运动 | 合计 | |
| 男性 | 21 | ||
| 女性 | 43 | 70 | |
| 合计 | 124 |
参考临界值表
| P(k2>k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
3.已知函数f(x)=$\frac{1}{3}{x^3}$+ax2+(a+2)x-3有两个极值点,则实数a的取值范围是( )
| A. | (-1,2) | B. | (-∞,-1)∪(2,+∞) | C. | [-1,2] | D. | (-∞,-1]∪[2,+∞) |