题目内容
12. 已知函数f(x)=x•|x|-2x.
已知函数f(x)=x•|x|-2x.(1)判断函数f(x)的奇偶性,并证明;
(2)求函数f(x)的零点;
(3)画出y=f(x)的图象,并结合图象写出方程f(x)=m有三个不同实根时,实数m的取值范围;
(4)写出函数f(x)的单调区间.
分析 (1)对于函数f(x),先分析其定义域,进而分析可得f(-x)=-f(x),即可证明函数f(x)为奇函数;
(2)令f(x)=0,x•|x|-2x=0,解可得x的值,由函数零点的定义,即可得答案;
(3)将f(x)的解析式变形可得f(x)=x•|x|-2x=$\left\{\begin{array}{l}{{x}^{2}-2x,x≥0}\\{{x}^{2}+2x,x<0}\end{array}\right.$,据此作出函数的图象;若方程f(x)=m有三个不同实根,则函数f(x)的图象与直线y=m有三个不同的交点,由图象可得实数m的取值范围;
(4)由图象,分析可得函数的单调区间,即可得答案.
解答 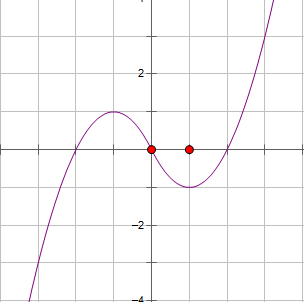 解:(1)函数f(x)为奇函数,
解:(1)函数f(x)为奇函数,
证明:对于函数f(x)=x•|x|-2x,其定义域为R,关于原点对称;
任取x∈R,-x∈R,
有f(-x)=-x•|-x|+2x=-x•|x|+2x,而-f(x)=-x•|x|+2x,
f(-x)=-f(x),
函数f(x)为奇函数;
(2)令f(x)=0,x•|x|-2x=0,
所以x(|x|-2)=0,
解得x=0或|x|=2
所以函数的零点为-2,0,2;
(3)f(x)=x•|x|-2x=$\left\{\begin{array}{l}{{x}^{2}-2x,x≥0}\\{{x}^{2}+2x,x<0}\end{array}\right.$,其图象如图:
若方程f(x)=m有三个不同实根,则函数f(x)的图象与直线y=m有三个不同的交点,
由图象可得实数m的取值范围为(-1,1);
(4)f(x)的单调递增区间为(-∞,-1),(1,+∞),f(x)的单调递减区间为(-1,1).
点评 本题考查分段函数的应用,涉及函数的奇偶性、单调性的判定,零点的求法,关键是理解函数的奇偶性、单调性以及零点的定义.

| A. | (-∞,0) | B. | (-∞,loga3) | C. | (0,+∞) | D. | (loga3,+∞) |
| A. | A⊆B | B. | B⊆A | C. | B?A | D. | A?B |
| A. | 相离 | B. | 相交 | C. | 相切 | D. | 不确定 |
| A. | $\frac{\sqrt{56}}{8}$ | B. | $\frac{\sqrt{85}}{7}$ | C. | $\frac{\sqrt{85}}{6}$ | D. | $\frac{\sqrt{13}}{3}$ |
| A. | -2 | B. | 0 | C. | 1 | D. | 2 |
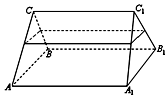 如图,一个三棱柱形容器中盛有水,且侧棱AA1=8.若侧面AA1B1B水平放置时,液面恰好过AC,BC,A1C1,B1C1的中点.则当底面ABC水平放置时,液面高为( )
如图,一个三棱柱形容器中盛有水,且侧棱AA1=8.若侧面AA1B1B水平放置时,液面恰好过AC,BC,A1C1,B1C1的中点.则当底面ABC水平放置时,液面高为( )