题目内容
2．已知变量x，y之间的一组数据如表：则y与x的线性回归直线必过点（ ）| x | 0 | 1 | 2 | 3 |
| y | 1 | 3 | 5 | 7 |
| A． | （$\frac{3}{2}$，4） | B． | （$\frac{3}{2}$，2） | C． | （1，4） | D． | （2，2） |
分析 本题是一个线性回归方程，这条直线的方程过这组数据的样本中心点，因此计算这组数据的样本中心点，做出x和y的平均数，得到结果．
解答 解：由题意知，y与x的线性回归方程必过样本中心点，
∵$\overline{x}$=$\frac{1}{4}×（0+1+2+3）$=1.5，$\overline{y}$=$\frac{1}{4}×（1+3+5+7）$=4，
∴线性回归方程必过（1.5，4）．
故选A．
点评 一组具有相关关系的变量的数据（x，y），通过散点图可观察出所有数据点都分布在一条直线附近，这样的直线可以画出许多条，而其中的一条能最好地反映x与y之间的关系，即这条直线“最贴近”已知的数据点，这就是回归直线．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
15．设向量$\overrightarrow{a}$=（n，1），$\overrightarrow{b}$=（2，1），且|$\overrightarrow{a}$-$\overrightarrow{b}$|2=|$\overrightarrow{a}$|2+|$\overrightarrow{b}$|2，则n=（ ）
| A． | -$\frac{1}{2}$ | B． | -2 | C． | 2 | D． | $\frac{1}{2}$ |
16．已知双曲线C$：\frac{x^2}{a^2}-\frac{y^2}{4}=1$的一条渐近线方程为2x+3y=0，F1，F2分别是双曲线C的左，右焦点，点P在双曲线C上，且|PF1|=7，则|PF2|等于（ ）
| A． | 1 | B． | 13 | C． | 4或10 | D． | 1或13 |
13．已知集合{x|x2+ax=0}={0，1}，则实数a的值为（ ）
| A． | -1 | B． | 0 | C． | 1 | D． | 2 |
7．若函数y=|x-2|-2的定义域为集合M={x∈R|-2≤x≤2}，值域为集合N，则（ ）
| A． | M=N | B． | M?N | C． | N?M | D． | M∩N=∅ |
14．
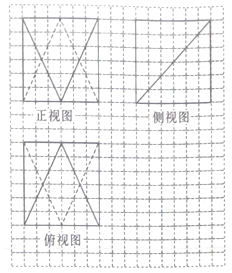如图，网格纸上小正方形的边长为1，粗实线及粗虚线画出的是某个多面体的三视图，则该多面体的体积为（ ）
如图，网格纸上小正方形的边长为1，粗实线及粗虚线画出的是某个多面体的三视图，则该多面体的体积为（ ）| A． | 72 | B． | $90\sqrt{3}$ | C． | $108\sqrt{2}$ | D． | 144 |
11．若a，b∈R，且a＞b，则下列不等式中恒成立的是（ ）
| A． | $\frac{1}{a}＜\frac{1}{b}$ | B． | a2＞b2 | C． | 2a＞2b | D． | $\frac{a}{b}＞1$ |
已知函数f（x）=x•|x|-2x．