题目内容
已知x，y满足不等式组
，则目标函数z=3x+y的最大值为（ ）
|
| A、12 | ||
| B、24 | ||
| C、8 | ||
D、
|
考点：简单线性规划
专题：不等式的解法及应用
分析：作出题中不等式组表示的平面区域，得如图的四边形OABC及其内部，再将目标函数z=2x+y对应的直线进行平移，可得当x=4，y=0时，z=3x+y取得最大值为12．
解答：
解：作出不等式组
表示的平面区域，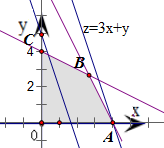
得到如图的四边形OABC及其内部，
其中O（0，0），A（4，0），B（
，
），C（0，8）
设z=F（x，y）=3x+y，将直线l：z=3x+y进行平移，
当l经过点A时，目标函数z达到最大值
∴z最大值=F（4，0）=12
故选：A．
|
得到如图的四边形OABC及其内部，
其中O（0，0），A（4，0），B（
| 8 |
| 3 |
| 8 |
| 3 |
设z=F（x，y）=3x+y，将直线l：z=3x+y进行平移，
当l经过点A时，目标函数z达到最大值
∴z最大值=F（4，0）=12
故选：A．
点评：本题给出二元一次不等式组，求目标函数z=3x+y的最大值，着重考查了二元一次不等式组表示的平面区域和简单的线性规划等知识，属于基础题．
练习册系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目
下列算式正确的是（ ）
| A、26+22=28 |
| B、26-22=24 |
| C、26×22=28 |
| D、26÷22=23 |
已知命题p：?x＜0，x2＞0，那么￢p是（ ）
| A、?x≥0，x2≤0 |
| B、?x≥0，x2≤0 |
| C、?x＜0，x2≤0 |
| D、?x≥0，x2≤0 |
已知集合M={x|2x≥1}，N={x||x|≤2}，则M∪N=（ ）
| A、[1，2] |
| B、[-2，+∞） |
| C、[0，2] |
| D、（0，2） |
下列命题正确的是（ ）
| A、若直线a与平面α不平行，则直线a与平面α内的所有直线都不平行 |
| B、如果两条直线在平面α内的射影平行，那么这两条直线平行 |
| C、垂直于同一直线的两个不同平面平行，垂直于同一平面的两条不同直线也平行 |
| D、直线a与平面α不垂直，则直线a与平面α内的所有直线都不垂直 |