题目内容
如图所示,△ABC中,∠B为直角,P是△ABC外一点,且PA=PB,PB⊥BC.若M是PC的中点,试确定AB上点N的位置,使得MN⊥AB.

[解析] ∵CB⊥AB,CB⊥PB,AB∩PB=B,
∴CB⊥平面APB.过M作ME∥CB,则ME⊥平面APB,∴ME⊥AB.若MN⊥AB,
∵ME∩MN=M,则AB⊥平面MNE,
∴AB⊥EN.取AB中点D,连结PD,
∵PA=PB,∴PD⊥AB,∴NE∥PD.
又M为PC中点,ME∥BC,∴E为PB中点.∵EN∥PD,
∴N为BD中点,故当N为AB的四等分点(AB=3BN)时,MN⊥AB.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
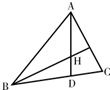 如图所示在△ABC中,sin2A+sin2C=sin2B+sinA.sinC
如图所示在△ABC中,sin2A+sin2C=sin2B+sinA.sinC 如图所示,△ABC中,AB=AC=2
如图所示,△ABC中,AB=AC=2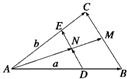 如图所示,△ABC中,
如图所示,△ABC中, 如图所示,△ABC中,已知顶点A(3,-1),∠B的内角平分线方程是x-4y+10=0过点C的中线方程为6x+10y-59=0.求顶点B的坐标和直线BC的方程.
如图所示,△ABC中,已知顶点A(3,-1),∠B的内角平分线方程是x-4y+10=0过点C的中线方程为6x+10y-59=0.求顶点B的坐标和直线BC的方程.