题目内容
 如图所示,△ABC中,AB=AC=2
如图所示,△ABC中,AB=AC=2| 3 |
| lim |
| n→∞ |
分析:设|AB1|=|BB1|=x,由余弦定理可知,x2+x2-2x2cos120°=12,解得x=2.由此可知a1=
.同理,由余弦定理可知3b12=
,所以能够求出a1+b1的值.同理可知a2+b2=
(
+1),a3+b3=
(
+1),…,an+bn=
(
+1)• (
)n-1,由此能够得到
[(a1+b1)+(a2+b2)+…+(an+bn)]的值.
4
| ||
| 3 |
| 48 |
| 9 |
| 8 |
| 9 |
| 3 |
| 16 |
| 27 |
| 3 |
| 4 |
| 3 |
| 3 |
| 2 |
| 3 |
| lim |
| n→∞ |
解答:解:∵AB=AC=2
,∠B1AB=∠B1BA=30°,B1A1∥BA,A1B2∥AB1,B2A2∥B1A1,A2B3∥A1B2,B3A3∥B2A2,….
设|AB1|=|BB1|=x,由余弦定理可知,x2+x2-2x2cos120°=12,解得x=2.
∵|BC|=
=6,
∴
=
,
∴a1=
.
同理,由余弦定理可知3b12=
,
∴b1=
.
∴a1+b1=
(
+1).
同理可知a2+b2=
(
+1),a3+b3=
(
+1),…,an+bn=
(
+1)• (
)n-1,
[(a1+b1)+(a2+b2)+…+(an+bn)]
=
[
(
+1)+
(
+1)+…+
(
+1)•(
)n-1]
=
(
+1) =4(
+1).
答案:
(
+1),4(
+1).
| 3 |
设|AB1|=|BB1|=x,由余弦定理可知,x2+x2-2x2cos120°=12,解得x=2.
∵|BC|=
| 12+12-2×12×cos120° |
∴
| a1 | ||
2
|
| 6-2 |
| 6 |
∴a1=
4
| ||
| 3 |
同理,由余弦定理可知3b12=
| 48 |
| 9 |
∴b1=
| 4 |
| 3 |
∴a1+b1=
| 4 |
| 3 |
| 3 |
同理可知a2+b2=
| 8 |
| 9 |
| 3 |
| 16 |
| 27 |
| 3 |
| 4 |
| 3 |
| 3 |
| 2 |
| 3 |
| lim |
| n→∞ |
=
| lim |
| n→∞ |
| 4 |
| 3 |
| 3 |
| 8 |
| 9 |
| 3 |
| 4 |
| 3 |
| 3 |
| 2 |
| 3 |
=
| ||
1-
|
| 3 |
| 3 |
答案:
| 4 |
| 3 |
| 3 |
| 3 |
点评:本题考查数列的综合知识,难度较大,解题时要认真审题,仔细解答.

练习册系列答案
相关题目
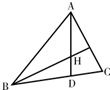 如图所示在△ABC中,sin2A+sin2C=sin2B+sinA.sinC
如图所示在△ABC中,sin2A+sin2C=sin2B+sinA.sinC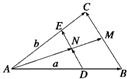 如图所示,△ABC中,
如图所示,△ABC中, 如图所示,△ABC中,已知顶点A(3,-1),∠B的内角平分线方程是x-4y+10=0过点C的中线方程为6x+10y-59=0.求顶点B的坐标和直线BC的方程.
如图所示,△ABC中,已知顶点A(3,-1),∠B的内角平分线方程是x-4y+10=0过点C的中线方程为6x+10y-59=0.求顶点B的坐标和直线BC的方程.