题目内容
5.已知tanα=$\frac{1}{3}$,则$\frac{sinα+2cosα}{5cosα-sinα}$=$\frac{1}{2}$.分析 由条件利用同角三角函数的基本关系,求得要求式子的值.
解答 解:∵tanα=$\frac{1}{3}$,则$\frac{sinα+2cosα}{5cosα-sinα}$=$\frac{tanα+2}{5-tanα}$=$\frac{\frac{7}{3}}{\frac{14}{3}}$=$\frac{1}{2}$,
故答案为:$\frac{1}{2}$.
点评 本题主要考查同角三角函数的基本关系,属于基础题.

练习册系列答案
相关题目
16.某几何体的三视图如图所示,则该几何体的体积等于( )
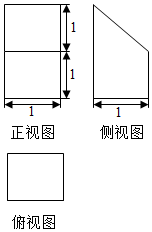

| A. | $\frac{3}{2}$ | B. | 2 | C. | $\frac{5}{2}$ | D. | 3 |
13.若a为实数且$\frac{2-ai}{i}$=-2-2i,则a=( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
20.某几何体的三视图如图所示,若这个几何体的体积为24,则h=( )


| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
10.在△ABC中,若a2-b2=$\sqrt{3}$bc,且$\frac{sin(A+B)}{sinB}$=2$\sqrt{3}$,则角A=( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |