题目内容
17.设a、b为正实数,且$\frac{1}{a}$+$\frac{1}{b}$=2$\sqrt{2}$.(1)求a2+b2的最小值;
(2)若(a-b)2≥4(ab)3,求ab的值.
分析 (1)根据基本不等式得出ab$≥\frac{1}{2}$(a=b时等号成立),
利用a2+b2≥2ab=$2×\frac{1}{2}=1$(a=b时等号成立)求解即可.
(2)根据$\frac{1}{a}$+$\frac{1}{b}$=2$\sqrt{2}$.
∴a$+b=2\sqrt{2}ab$,
代入得出(a+b)2-4ab≥4(ab)3,即(2$\sqrt{2}ab$)2-4ab≥4(ab)3
求解即可得出ab=1
解答 解:(1)∵a、b为正实数,且$\frac{1}{a}$+$\frac{1}{b}$=2$\sqrt{2}$.
∴a、b为正实数,且$\frac{1}{a}$+$\frac{1}{b}$=2$\sqrt{2}$≥2$\sqrt{\frac{1}{ab}}$(a=b时等号成立).
即ab$≥\frac{1}{2}$(a=b时等号成立)
∵a2+b2≥2ab=$2×\frac{1}{2}=1$(a=b时等号成立).
∴a2+b2的最小值为1,
(2)∵且$\frac{1}{a}$+$\frac{1}{b}$=2$\sqrt{2}$.
∴a$+b=2\sqrt{2}ab$
∵(a-b)2≥4(ab)3,
∴(a+b)2-4ab≥4(ab)3
即(2$\sqrt{2}ab$)2-4ab≥4(ab)3
即(ab)2-2ab+1≤0,(ab-1)2≤0,
∵a、b为正实数,
∴ab=1
点评 本题考查了基本不等式,考查了运用基本不等式求函数的最值,运用基本不等式求函数最值时,要保证:“一正、二定、三相等”,此题是基础题

练习册系列答案
相关题目
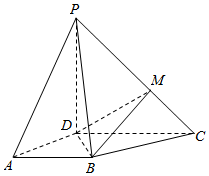 如图,四棱锥P-ABCD中,PD⊥底面ABCD,AB∥CD,∠BAD=$\frac{π}{3}$,AB=2,CD=3,M为PC上一点,PM=2MC.
如图,四棱锥P-ABCD中,PD⊥底面ABCD,AB∥CD,∠BAD=$\frac{π}{3}$,AB=2,CD=3,M为PC上一点,PM=2MC.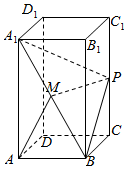 如图,在正四棱柱ABCD-A1B1C1D1中,AD=1,D1D=2,点P为棱CC1的中点.
如图,在正四棱柱ABCD-A1B1C1D1中,AD=1,D1D=2,点P为棱CC1的中点.