题目内容
16.设平面向量$\overrightarrow a$=( m,1),$\overrightarrow b$=( 2,n ),其中 m,n∈{-2,-1,1,2}.(I)记“使得$\overrightarrow a$⊥$\overrightarrow b$成立的( m,n )”为事件A,求事件A发生的概率;
(II)记“使得$\overrightarrow a$∥($\overrightarrow a$-2$\overrightarrow b$)成立的( m,n )”为事件B,求事件B发生的概率.
分析 (Ⅰ)先求出基本事件总数N=4×4=16,由$\overrightarrow{a}$⊥$\overrightarrow{b}$,得m=-2n,由此利用列举法求出事件A包含的基本事件(m,n)的个数,由此能求出事件A发生的概率P(A).
(Ⅱ)先求出$\overrightarrow{a}-2\overrightarrow{b}$=(m-4,1-2n),再由$\overrightarrow a$∥($\overrightarrow a$-2$\overrightarrow b$),求出mn=2,利用列举法求出事件B包含的基本事件(m,n)的个数,由此能求出事件B发生的概率P(B).
解答 解:(Ⅰ)∵m,n∈{-2,-1,1,2},
∴基本事件总数N=4×4=16,
记“使得$\overrightarrow a$⊥$\overrightarrow b$成立的( m,n )”为事件A,
由平面向量$\overrightarrow a$=( m,1),$\overrightarrow b$=( 2,n ),$\overrightarrow{a}$⊥$\overrightarrow{b}$,
得$\overrightarrow{a}•\overrightarrow{b}$=2m+n=0,即m=-2n,
∴事件A包含的基本事件(m,n)有:(-2,1)(2,-1),共2个,
∴事件A发生的概率P(A)=$\frac{2}{16}$=$\frac{1}{8}$.
(Ⅱ)记“使得$\overrightarrow a$∥($\overrightarrow a$-2$\overrightarrow b$)成立的( m,n )”为事件B,
由$\overrightarrow{a}-2\overrightarrow{b}$=(m-4,1-2n),$\overrightarrow a$∥($\overrightarrow a$-2$\overrightarrow b$),
得$\frac{m}{m-4}=\frac{1}{1-2n}$,即mn=2,
∴事件B包含的基本事件(m,n)有:(-2,-1),(-1,-2),(1,2),(2,1),共4个,
∴事件B发生的概率P(B)=$\frac{4}{16}=\frac{1}{4}$.
点评 本题考查概率的求法,涉及到平面向量坐标运算法则、向量平行的性质的应用、等可能事件概率计算公式等基础知识,考查推理论证能力、运算求解能力,考查函数与方程思想,是基础题.

 阅读快车系列答案
阅读快车系列答案 执行一次如图所示的程序框图,若输出i的值为0,则下列关于框图中函数f(x)(x∈R)的表述,正确的是( )
执行一次如图所示的程序框图,若输出i的值为0,则下列关于框图中函数f(x)(x∈R)的表述,正确的是( )| A. | f(x)是奇函数,且为减函数 | B. | f(x)是偶函数,且为增函数 | ||
| C. | f(x)不是奇函数,也不为减函数 | D. | f(x)不是偶函数,也不为增函数 |

(Ⅰ)现对该市市民进行“经常使用共享单车与年龄关系”的调查,采用随机抽样的方法,抽取一个容量为200的样本,请你根据图表中的数据,补全下列2×2列联表,并根据列联表的独立性检验,判断能有多大把握可以认为经常使用共享单车与年龄有关?
使用共享单车情况与年龄列联表
| 年轻人 | 非年轻人 | 合计 | |
| 经常使用共享单车用户 | 120 | ||
| 不常使用共享单车用户 | 80 | ||
| 合计 | 160 | 40 | 200 |
(参考数据:
| P(K2≥k0) | 0.15 | 0.10 | 0.050 | 0.025 | 0.010 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
| A. | (-∞,-2)∪(2,+∞) | B. | (-∞,-1)∪(1,+∞) | C. | (-2,2) | D. | (-1,1) |

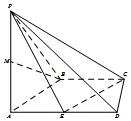 如图,在四棱锥P-ABCD中,AD∥BC,BC⊥CD,点P在底面ABCD上的射影为A,BC=CD=$\frac{1}{2}$AD=1,E为棱AD的中点,M为棱PA的中点.
如图,在四棱锥P-ABCD中,AD∥BC,BC⊥CD,点P在底面ABCD上的射影为A,BC=CD=$\frac{1}{2}$AD=1,E为棱AD的中点,M为棱PA的中点.