Question

【题目】已知椭圆过点，且离心率为.过抛物线上一点作的切线交椭圆于，两点.

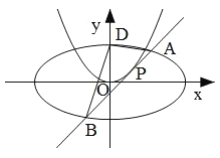
（Ⅰ）求椭圆的方程；

（Ⅱ）是否存在直线，使得，若存在，求出的方程；若不存在，请说明理由.

Answer 1

【答案】（Ⅰ）椭圆（Ⅱ）见解析

【解析】

（Ⅰ）根据已知条件列有关a、b、c的方程组，求出a和b的值，即可得出椭圆C1的方程；

（Ⅱ）设直线l的方程为y＝kx+t，先利用导数写出直线l的方程，于是得到k＝2x0，，将直线l的方程与椭圆C1的方程联立，列出韦达定理，由并代入韦达定理，通过计算得出t的值，可得出x0的值，从而可得出直线l的方程．

（Ⅰ）由题知，得,

所以椭圆,

（Ⅱ）设的方程：,

由求导可得，的方程：,

故 . 由，得.

所以,

由题意可知：

即(4t2-4)(k2+1)-8k2t(t-1)+(t-1)2(4k2+1)=0,

化简有5t2-2t-3=0，所以t=1或t=,

，

此时，l方程：，经检验，直线l符合题意