Question

【题目】设等差数列的前项和为，数列的前项和为，下列说法错误的是（ ）

A. 若有最大值，则也有最大值

B. 若有最大值，则也有最大值

C. 若数列不单调，则数列也不单调

D. 若数列不单调，则数列也不单调

Answer 1

【答案】C

【解析】

根据等差数列的性质知数列{a2n﹣1}的首项是a1，公差为2d，结合等差数列的前n项和公式以及数列的单调性和最值性与首项公差的关系进行判断即可．

解：数列{a2n﹣1}的首项是a1，公差为2d，

A．若Sn有最大值，则满足a1＞0，d＜0，则2d＜0，即Tn也有最大值，故A正确，

B．若Tn有最大值，则满足a1＞0，2d＜0，则d＜0，即Sn也有最大值，故B正确，

C．Sn＝na1dn2+（a1）n，对称轴为n，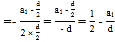

Tn＝na12d＝dn2+（a1﹣d）n，对称轴为n，

不妨假设d＞0，

若数列{Sn}不单调，此时对称轴n，即1，

此时Tn的对称轴n1，则对称轴有可能成立，此时数列{Tn}有可能单调递增，

故C错误，

D．不妨假设d＞0，若数列{Tn}不单调，此时对称轴n，即2，

此时{Sn}的对称轴n2，即此时{Sn}不单调，故D正确

则错误是C，

故选：C．