Question

如图，PQ为半圆O的直径，A为以OQ为直径的半圆A的圆心，圆O的弦PN切圆A于点M，PN=8，则圆A的半径为

 

．

Answer 1

考点：圆的切线的性质定理的证明

专题：立体几何

分析：利用圆的直径的性质、圆的切线的性质可得：∠PNQ=90°=∠PMA．进而得到AM∥QN，可得

PM

PN

=

PA

PQ

=

3

4

．可得PM，再根据切割线定理可得：PM²=PO•PQ．可得PO．

解答： 解：如图所示，连接AM，QN．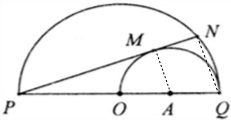
由于PQ是⊙O的直径，∴∠PNQ=90°．
∵圆O的弦PN切圆A于点M，∴AM⊥PN．
∴AM∥QN，
∴

PM

PN

=

PA

PQ

=

3

4

．
又PN=8，∴PM=6．
根据切割线定理可得：PM²=PO•PQ．
设⊙O的半径为R．则6²=R•2R，
∴R=3

2

，
∴⊙A的半径r=

1

2

R=

3 2

2

．
故答案为：

3 2

2

．

点评：本题考查了圆的直径的性质、圆的切线的性质、平行线分线段成比例定理、切割线定理，属于基础题．