题目内容
已知向量a＝(cosλθ，cos(10－λ)θ)，b＝(sin(10－λ)θ，sinλθ)，λ、θ∈R.
(1) 求|a|2＋|b|2的值；
(2) 若a⊥b，求θ；
(3) 若θ＝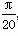
，求证：a∥b.
(1) 解：∵ |a|＝
|b|＝
，
∴ |a|2＋|b|2＝2.
(2) 解：∵ a⊥b，
∴ cosλθ·sin(10－λ)θ＋cos(10－λ)θ·sinλθ＝0，
∴ sin[(10－λ)θ＋λθ]＝0，∴ sin10θ＝0，
∴ 10θ＝kπ，k∈Z，∴ θ＝
，k∈Z.
(3) 证明：∵ θ＝
，
cosλθ·sinλθ－cos(10－λ)θ·sin[(10－λ)θ]
＝cos
·sin－cos
·sin
＝cos·sin－sin·cos＝0，∴ a∥b.
练习册系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
(n∈N*)，则a20＝( )
＋i，ω＝sinθ－icosθ(θ∈R)．求z的值和|z－ω|的取值范围．
b，m∈R，k、t为正实数．
，BC＝2，点E为BC的中点，点F在边CD上．若
＝
＝________．
，求
＋
的值．
.
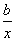