题目内容
设f(x)和g(x)都是定义在同一区间上的两个函数,若对任意x∈[1,2],都有|f(x)+g(x)|≤8,则称f(x)和g(x)是“友好函数”,设f(x)=ax,g(x)=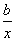 .
.
(1)若a∈{1,4},b∈{-1,1,4},求f(x)和g(x)是“友好函数”的概率;
(2)若a∈[1,4],b∈[1,4],求f(x)和g(x)是“友好函数”的概率.
解析: (1)设事件A表示f(x)和g(x)是“友好函数”,
则|f(x)+g(x)|(x∈[1,2])所有的情况有:
x-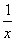 ,x+
,x+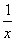 ,x+
,x+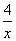 ,4x-
,4x-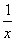 ,4x+
,4x+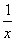 ,4x+
,4x+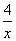 ,
,
共6种且每种情况被取到的可能性相同.
又当a>0,b>0时,ax+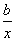 在
在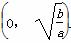 上递减,在
上递减,在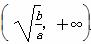 上递增;
上递增;
x-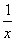 和4x-
和4x-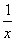 在(0,+∞)上递增,
在(0,+∞)上递增,
∴对x∈[1,2]可使|f(x)+g(x)|≤8恒成立的有x-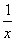 ,x+
,x+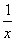 ,x+
,x+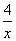 ,4x-
,4x-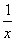 ,故事件A包含的基本事件有4种,
,故事件A包含的基本事件有4种,
∴P(A)= =
= ,故所求概率是
,故所求概率是 .
.
(2)设事件B表示f(x)和g(x)是“友好函数”,
∵a是从区间[1,4]中任取的数,b是从区间[1,4]中任取的数,
∴点(a,b)所在区域是长为3,宽为3的矩形区域.
要使x∈[1,2]时,|f(x)+g(x)|≤8恒成立,
需f(1)+g(1)=a+b≤8且f(2)+g(2)=2a+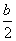 ≤8,
≤8,
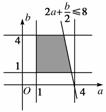
∴事件B表示的点的区域是如图所示的阴影部分.
∴P(B)=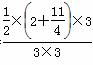 =
=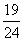 ,
,
故所求概率是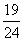 .
.

练习册系列答案
相关题目
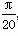 ,求证:a∥b.
,求证:a∥b.
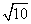 ,则|b|=( )
,则|b|=( )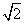 B.2
B.2 ,且|a|=1,|b|=4,若(2a+λb)⊥a,则实数λ=________.
,且|a|=1,|b|=4,若(2a+λb)⊥a,则实数λ=________. B.6
B.6