题目内容
已知向量a=(1,2),b=(-2,m),x=a+(t2+1)b,y=-ka+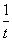 b,m∈R,k、t为正实数.
b,m∈R,k、t为正实数.
(1) 若a∥b,求m的值;
(2) 若a⊥b,求m的值;
(3) 当m=1时,若x⊥y,求k的最小值.
解:(1) 因为a∥b,所以1·m-2·(-2)=0,解得m=-4.
(2) 因为a⊥b,所以a·b=0,
所以1·(-2)+2m=0,解得m=1.
(3) 当m=1时,a·b=0.
因为x⊥y,所以x·y=0.
则x·y=-ka2+ a·b+(t+
a·b+(t+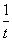 )b2=0.
)b2=0.
因为t>0,所以k=t+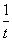 ≥2,当t=1时取等号,
≥2,当t=1时取等号,
即k的最小值为2.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目

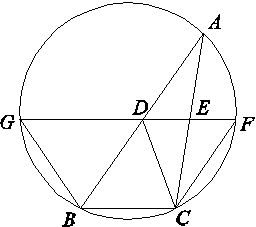
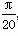 ,求证:a∥b.
,求证:a∥b. =________.
=________.