题目内容
若 ,则( )
,则( )
A. < < < < | B. < < < < |
C. < < < < | D. < < < < |
C
解析试题分析:因为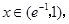 所以
所以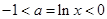 ,而
,而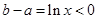 ,故
,故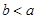 ,又
,又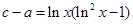 ,而
,而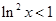 ,故
,故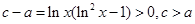 ,综上,
,综上,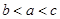 ,选C.
,选C.
考点:对数函数.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案
相关题目
已知 是R上的单调递增函数,则实数
是R上的单调递增函数,则实数 的取值范围为 ( )
的取值范围为 ( )
| A.(1,+∞) | B.[4,8) | C.(4,8) | D.(1,8) |
设函数 在
在 内有定义,对于给定的正数k,定义函数:
内有定义,对于给定的正数k,定义函数:
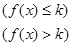 ,取函数
,取函数 ,若对任意的
,若对任意的 ,恒有
,恒有 ,则( )
,则( )
A. 的最大值为2 的最大值为2 | B. 的最小值为2 的最小值为2 | C. 的最大值为1 的最大值为1 | D. 的最小值为1 的最小值为1 |
对实数a和b,定义运算“?”:a?b= ,设函数f(x)=(x2-2)?(x-x2),x∈R,若函数y=f(x)-c的图象与x轴恰有两个公共点,则实数c的取值范围是( )
,设函数f(x)=(x2-2)?(x-x2),x∈R,若函数y=f(x)-c的图象与x轴恰有两个公共点,则实数c的取值范围是( )
A.(-∞,-2]∪ | B.(-∞,-2]∪ |
C. ∪ ∪ | D. ∪ ∪ |
设函数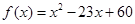 ,
, ,则
,则 ( )
( )
| A.0 | B.38 | C.56 | D.112 |
若 ,则函数
,则函数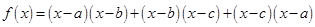 的两个零点分别位于区间 ( )
的两个零点分别位于区间 ( )
A. 和 和 内 内 | B. 和 和 内 内 |
C. 和 和 内 内 | D. 和 和 内 内 |
已知函数 ,则函数
,则函数 的零点个数是( )
的零点个数是( )
| A.4 | B.3 | C.2 | D.1 |
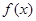 满足:当
满足:当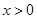 时,
时,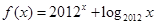 ,则在R上,函数
,则在R上,函数 的定义域为D,若对于任意
的定义域为D,若对于任意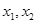
 ,当
,当 时,都有
时,都有 ,则称函
,则称函 ; ②
; ② ; ③
; ③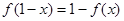 .
.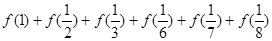 等于( )
等于( )

