题目内容
函数 的定义域为D,若对于任意
的定义域为D,若对于任意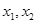
 ,当
,当 时,都有
时,都有 ,则称函
,则称函
数 在D上为非减函数,设函数
在D上为非减函数,设函数 在[0,1]上为非减函数,且满足以下三个条件:
在[0,1]上为非减函数,且满足以下三个条件:
① ; ②
; ② ; ③
; ③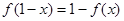 .
.
则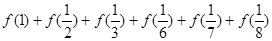 等于( )
等于( )
A. | B. | C. | D.无法确定 |
A
解析试题分析:由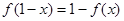 ,令
,令 ,得
,得 ,因为
,因为 ,所以
,所以 .由②,令
.由②,令 ,得
,得 .由③,令
.由③,令 ,得
,得 ,所以
,所以 .再由②,令
.再由②,令 ,得
,得 .②中再令
.②中再令 ,得
,得 .又函数
.又函数 在[0,1]上为非减函数,
在[0,1]上为非减函数, ,所以
,所以 ,故
,故 .所以有
.所以有 =1+
=1+ +
+ +
+ +
+ +
+ =
= .
.
考点:抽象函数的运算、新概念的理解

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
函数 的零点的个数( )
的零点的个数( )
| A.4 | B.3 | C.2 | D.1 |
已知函数 的定义域为
的定义域为 ,则函数
,则函数 的定义域是( )
的定义域是( )
| A.[1,2] | B.[0,4] | C.(0,4] | D.[ ,4] ,4] |
已知点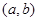 在函数
在函数 的图像上 , 则下列点中不可能在此图像上的是( )
的图像上 , 则下列点中不可能在此图像上的是( )
A. | B. | C. | D. |
已知函数 ,
, ,
, ,则
,则 的最小值等于( ).
的最小值等于( ).
A. | B. | C. | D. |
若 ,则( )
,则( )
A. < < < < | B. < < < < |
C. < < < < | D. < < < < |
如果函数 在区间
在区间 上是减少的,那么实数
上是减少的,那么实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
 则
则 的大致图象是( )
的大致图象是( )
 上,函数
上,函数 ,
, ,
, ,
, 中有三个是增函数;②若
中有三个是增函数;②若 ,则
,则 ;③若函数
;③若函数 是奇函数,则
是奇函数,则 的图象关于点
的图象关于点 对称;④已知函数
对称;④已知函数 则方程
则方程 有
有 个实数根,其中正确命题的个数为( )
个实数根,其中正确命题的个数为( )

