题目内容
8．“a=-1”是“函数f（x）=x2-2ax-1在区间[-1，+∞）上为增函数”的（ ）| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
分析 根据函数单调性的性质求出对称性和单调区间的关系，结合充分条件和必要条件的定义进行判断．
解答 解：若f（x）=x2-2ax-1在区间[-1，+∞）上为增函数，
则对称性x=-$\frac{-2a}{2}$=a≤-1，
则“a=-1”是“函数f（x）=x2-2ax-1在区间[-1，+∞）上为增函数”的充分不必要条件，
故选：A．
点评 本题主要考查充分条件和必要条件的定义结合函数单调性的关系是解决本题的关键．
练习册系列答案
相关题目
3．在区间（0，100）上任取一数x，则lg x＞1的概率是（ ）
| A． | 0.1 | B． | 0.5 | C． | 0.8 | D． | 0.9 |
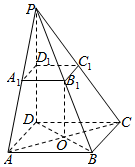在四棱锥P-ABCD中，底面ABCD是菱形，PD⊥平面ABCD，点D1为棱PD的中点，过D1作与平面ABCD平行的平面与棱PA，PB，PC相交于A1，B1，C1，∠BAD=60°．