题目内容
16.已知a>0且a≠1,x>0,下列关于三个函数f(x)=ax,g(x)=xa,h(x)=logax的说法正确的是( )| A. | 三个函数的单调性总相同 | |
| B. | 当1<a<2时,对任意x>0,f(x)>g(x)>h(x) | |
| C. | 当a>1时,三个函数没有公共点 | |
| D. | 任意a>1,三个函数都与直线y=x相交 |
分析 A根据指数函数,对数函数和幂函数的性质判断;
B可取特例进行判断;
C根据指数函数和对数函数互为反函数以及指数函数的性质可判断;
D根据C选项可直接判断.
解答 解:A中f(x)=ax,h(x)=logax的单调性是相同的,有增有减,但g(x)=xa在a>0且a≠1上,在定义域内都是递增的,故错误;
B中当1<a<2时,不妨令a=$\frac{3}{2}$,显然可知f(4)<g(4),故错误;
C中当a>1时,f(x)=ax中y都大于x,在直线y=x上方,根据反函数关于y=x对称可知h(x)=logax在y=x下方,故没有公共点,故正确;
D中显然当a=32时,f(x)=ax不与直线y=x相交,故错误.
故选:C.
点评 考查了指数函数,对数函数和幂函数的性质以及对性质的应用.应理解做题思路和判断方法.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
6.已知抛物线C的顶点在坐标原点,准线方程为x=-1,直线l与抛物线C相交于A,B两点.若线段AB的中点为(2,1),则直线l的方程为( )
| A. | y=2x-3 | B. | y=2x-1 | C. | y=x-3 | D. | y=x-1 |
7.设命题p:函数f(x)=ex在R上为增函数;命题q:函数f(x)=cos2x为奇函数,则下列命题中真命题是( )
| A. | p∧q | B. | (¬p)∨q | C. | (¬p)∧(¬q) | D. | p∧(¬q) |
11.已知i为虚数单位,满足z(1+2i)=3+4i,则复数z所在的象限为( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
1.若复数z满足1+z=i,则|z|=( )
| A. | $\sqrt{2}$ | B. | 1 | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{1}{2}$ |
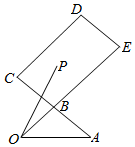 如图,B是AC的中点,$\overrightarrow{BE}$=2$\overrightarrow{OB}$,P是矩形BCDE内(含边界)的一点,且$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$(x,y∈R).则x-y的最大值为-1.
如图,B是AC的中点,$\overrightarrow{BE}$=2$\overrightarrow{OB}$,P是矩形BCDE内(含边界)的一点,且$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$(x,y∈R).则x-y的最大值为-1.