题目内容
8.已知双曲线C的方程$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{5}$=1,其左、右焦点分别是F1,F2,已知点M坐标为(2,1).双曲线C上点P(x0,y0)(x0>0,y0>0)满足$\overrightarrow{OM}$=$\overrightarrow{OP}$+λ($\frac{\overrightarrow{P{F}_{1}}}{|\overrightarrow{P{F}_{1}}|}$+$\frac{\overrightarrow{P{F}_{2}}}{|P{F}_{2}|}$),则S${\;}_{△PM{F}_{1}}$-S${\;}_{△PM{F}_{2}}$=2.分析 求出双曲线的a,b,c,设△PF1F2的内切圆与三边的切点分别是D,E,H,运用切线的性质:切线长相等,结合双曲线的定义,可得内心的横坐标为a,由向量的平行四边形法则可得M在∠F1PF2的平分线上,即有M为内心,运用三角形的面积公式,结合双曲线的定义,计算即可得到所求值.
解答 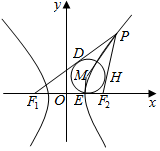 解:双曲线C的方程$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{5}$=1的a=2,b=$\sqrt{5}$,c=3.
解:双曲线C的方程$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{5}$=1的a=2,b=$\sqrt{5}$,c=3.
如右图,设△PF1F2的内切圆与三边的切点分别是D,E,H,
由切线的性质可得,PD=PH,F1D=F1E,F2E=F2H,
由双曲线的定义可得,PF1-PF2=2a,
即为F1D-F2H=2a,又F1D+F2H=F2E+F1E=F1F2=2c,
解得F1E=F1D=a+c,可得E的横坐标为a,
由$\overrightarrow{OM}$=$\overrightarrow{OP}$+λ($\frac{\overrightarrow{P{F}_{1}}}{|\overrightarrow{P{F}_{1}}|}$+$\frac{\overrightarrow{P{F}_{2}}}{|P{F}_{2}|}$),
可得$\overrightarrow{PM}$=λ($\frac{\overrightarrow{P{F}_{1}}}{|\overrightarrow{P{F}_{1}}|}$+$\frac{\overrightarrow{P{F}_{2}}}{|P{F}_{2}|}$),即有M在∠F1PF2的平分线上,
由于M(2,1),由a=2,可得M为内心,且半径为1,
则S${\;}_{△PM{F}_{1}}$-S${\;}_{△PM{F}_{2}}$=$\frac{1}{2}$r(PF1-PF2)=$\frac{1}{2}$•1•2a=a=2.
故答案为:2.
点评 本题考查向量知识的运用,考查三角形面积的计算,注意运用切线的性质和双曲线的定义,考查学生运算求解和分析解决问题的能力,属于中档题.

 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案| A. | $\frac{\sqrt{5}}{2}$ | B. | $\sqrt{2}$ | C. | 2$\sqrt{2}$ | D. | $\sqrt{5}$ |
| A. | a>c>b | B. | a>b>c | C. | c>a>b | D. | c>b>a |
| A. | 三个函数的单调性总相同 | |
| B. | 当1<a<2时,对任意x>0,f(x)>g(x)>h(x) | |
| C. | 当a>1时,三个函数没有公共点 | |
| D. | 任意a>1,三个函数都与直线y=x相交 |
| A. | f($\sqrt{2}$)<f(2)<f(3) | B. | f(2)<f(3)<f($\sqrt{2}$) | C. | f(3)<f(2)<f($\sqrt{2}$) | D. | f(3)<f($\sqrt{2}$)<f(2) |
| A. | 0 | B. | 6$\sqrt{2}$ | C. | 36 | D. | 72 |
| A. | 2 | B. | 6 | C. | 15 | D. | 20 |
| A. | p∧q | B. | (¬p)∧q | C. | p∧(¬q) | D. | (¬p)∧(¬q) |