题目内容
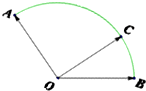 如图,在圆心角为120°的扇形中,以圆心O为起点作射线OC,则使得∠AOC与∠BOC都不大于90°的概率是( )
如图,在圆心角为120°的扇形中,以圆心O为起点作射线OC,则使得∠AOC与∠BOC都不大于90°的概率是( )A、
| ||
B、
| ||
C、
| ||
D、
|
考点:几何概型
专题:概率与统计
分析:求出∠AOC和∠BOC中为直角的位置,利用几何概型的概率公式即可得到结论.
解答:
解:过O分别作OE⊥OB,OD⊥OA,
则∠BOE=∠AOD=90°,
当点C位于弧DE,∠AOC和∠BOC中都不大于90°,
此时 ∠AOE=∠BOD=30°,
∠AOE=∠BOD=30°,
即∠DOE=120°-30°-30°=60°,
此时对应的概率P=
=
故选:C.
则∠BOE=∠AOD=90°,
当点C位于弧DE,∠AOC和∠BOC中都不大于90°,
此时
 ∠AOE=∠BOD=30°,
∠AOE=∠BOD=30°,即∠DOE=120°-30°-30°=60°,
此时对应的概率P=
| 60 |
| 120 |
| 1 |
| 2 |
故选:C.
点评:本题主要考查几何概型的概率计算,求出∠AOC与∠BOC都不大于90°的等价条件是解决本题的关键.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
已知圆O的方程为x2+y2=2,圆M的方程为(x-1)2+(y-3)2=1,过圆M上任意一点P做圆O的切线PA,若直线PA与圆M的另一个交点为Q,则当弦PQ的长度最大时,直线PA的斜率为( )
| A、k=-1或k=-7 |
| B、k=-1或k=7 |
| C、k=1或k=-7 |
| D、k=1或k=7 |
直线ax+
y+2=0与圆x2+y2=r2相切,则圆的半径最大时,a的值是( )
| 1 |
| a |
| A、1 | B、-1 |
| C、±1 | D、a可为任意非零实数 |
已知点A(3,6),B(2,4),则直线AB的斜率是( )
| A、1 | B、2 | C、3 | D、4 |
按如图的程序框图运行后,输出的S应为( )


| A、7 | B、15 | C、26 | D、40 |
直线2x-y+2=0与坐标轴围成的三角形的面积是( )
A、
| ||
| B、1 | ||
| C、2 | ||
| D、4 |
已知圆C1:(x+3)2+y2=1和圆C2:(x-3)2+y2=9,动圆M同时与圆C1及圆C2相外切,则动圆圆心M的轨迹方程是( )
A、x2-
| ||||
B、
| ||||
C、x2+
| ||||
D、
|