题目内容
8.若$\frac{1}{3}<x<\frac{1}{2}$是不等式m-1<x<m+1成立的一个充分非必要条件,则实数m的取值范围是$[-\frac{1}{2},\frac{4}{3}]$.分析 $\frac{1}{3}<x<\frac{1}{2}$是不等式m-1<x<m+1成立的一个充分非必要条件,可得$\left\{\begin{array}{l}{m-1≤\frac{1}{3}}\\{\frac{1}{2}≤m+1}\end{array}\right.$,等号不能同时成立,解出即可得出.
解答 解:∵$\frac{1}{3}<x<\frac{1}{2}$是不等式m-1<x<m+1成立的一个充分非必要条件,
∴$\left\{\begin{array}{l}{m-1≤\frac{1}{3}}\\{\frac{1}{2}≤m+1}\end{array}\right.$,且等号不能同时成立,
解得$-\frac{1}{2}≤m≤\frac{4}{3}$.
故答案为:$[-\frac{1}{2},\frac{4}{3}]$.
点评 本题考查了简易逻辑的判定方法、不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
16.焦点在y轴的椭圆x2+ky2=1的长轴长是短轴长的2倍,那么k等于( )
| A. | -4 | B. | $-\frac{1}{4}$ | C. | 4 | D. | $\frac{1}{4}$ |
13.若一个圆锥的底面半径是母线长的一半,侧面积和它的体积的数值相等,则该圆锥的底面半径为( )
| A. | $\sqrt{3}$ | B. | $2\sqrt{2}$ | C. | $2\sqrt{3}$ | D. | $4\sqrt{3}$ |
17.函数$f(x)={log_3}x-{(\frac{1}{2})^{x-2}}$的零点所在区间为( )
| A. | (3,4) | B. | (2,3) | C. | (1,2) | D. | (0,1) |
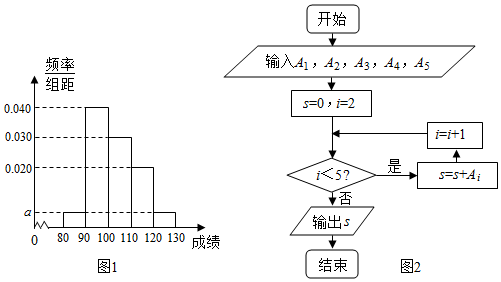
18.设x1=18,x2=19,x3=20,x4=21,x5=22,将这五个数据依次输入下边程序框进行计算,则输出的S值及其统计意义分别是( )

| A. | S=2,即5个数据的方差为2 | B. | S=2,即5个数据的标准差为2 | ||
| C. | S=10,即5个数据的方差为10 | D. | S=10,即5个数据的标准差为10 |
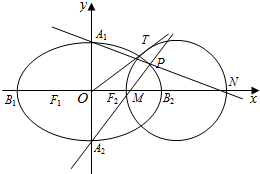 已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率$e=\frac{{\sqrt{3}}}{2}$,椭圆C的上、下顶点分别为A1,A2,左、右顶点分别为B1,B2,左、右焦点分别为F1,F2.原点到直线A2B2的距离为$\frac{2\sqrt{5}}{5}$.
已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率$e=\frac{{\sqrt{3}}}{2}$,椭圆C的上、下顶点分别为A1,A2,左、右顶点分别为B1,B2,左、右焦点分别为F1,F2.原点到直线A2B2的距离为$\frac{2\sqrt{5}}{5}$.