题目内容
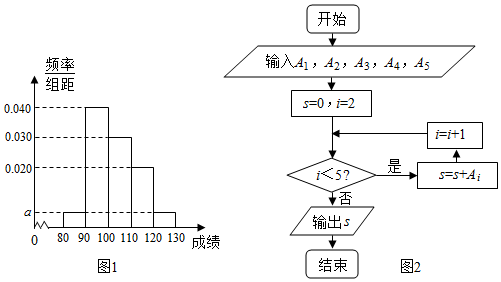
20.从某企业生产的某种产品中抽取20件,测量这些产品的一项质量指标值,由测量得到如图1的频率分布直方图,从左到右各组的频数依次记为A1,A2,A3,A4,A5.(1)求图中a的值并估算该企业产品质量指标的平均值;
(2)如图2是统计图中各组频数的一个算法流程图,求输出的结果S;
(3)从质量指标值分布在[80,90),[110,120)的产品中随机抽取2件产品,求所抽取两件产品的质量指标值之差大于10的概率.
分析 (1)依题意,利用频率之和为1,直接求解a的值.累指各组组中与频率的乘积,可得平均值的估算值;
(2)由频率分布直方图可求A1,A2,A3,A4,A5的值,由程序框图可得S=A2+A3+A4,代入即可求值.
(3)记质量指标在[110,120)的4件产品为x1,x2,x3,x4,质量指标在[80,90)的1件产品为y1,可得从5件产品中任取2件产品的结果共10种,记“两件产品的质量指标之差大于10”为事件A,可求事件A中包含的基本事件共4种,从而可求得P(A).
解答 解:(1)依题意,(2a+0.02+0.03+0.04)×10=1
解得:a=0.005,
由(0.005×85+0.02×115+0.03×105+0.04×95+0.005×125)×10=103,
故该企业产品质量指标的平均值约为103件;
(2)A1=0.005×10×20=1,A2=0.040×10×20=8,A3=0.030×10×20=6,A4=0.020×10×20=4,A5=0.005×10×20=1
故输出的S=A2+A3+A4=18
(3)记质量指标在[110,120)的4件产品为x1,x2,x3,x4,质量指标在[80,90)的1件产品为y1,
则从5件产品中任取2件产品的结果为:(x1,x2),(x1,x3),(x1,x4),(x1,y1),(x2,x3),
(x2,x4),(x2,y1),(x3,x4),(x3,y1),(x4,y1)共10种,
记“两件产品的质量指标之差大于10”为事件A,
则事件A中包含的基本事件为:(x1,y1),(x2,y1),(x3,y1),(x4,y1)共4种
所以可得:P(A)=$\frac{4}{10}$=$\frac{2}{5}$.
即从质量指标值分布在[80,90)、[110,120)的产品中随机抽取2件产品,所抽取两件产品的质量指标之差大于10的概率为$\frac{2}{5}$
点评 本题考查读频率分布直方图的能力和利用统计图获取信息的能力,利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题,属于中档题.


| A. | 0 | B. | -1 | C. | 1 | D. | 17 |
| A. | 7,9 | B. | 5,11 | C. | 7,11 | D. | 5,9 |
| A. | M=P | B. | M?P | C. | P?M | D. | M∈P |
| A. | $2\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{6}$ |
| A. | 一般茎叶图左侧的叶按从小到大的顺序写,右侧的数据按从小到大的顺序写,相同的数据可以只记一次 | |
| B. | 系统抽样在第一段抽样时一般采用简单随机抽样 | |
| C. | 两个事件的和事件是指两个事件都发生的事件 | |
| D. | 分层抽样每个个体入样可能性不同 |