题目内容
已知关于x不等式2x-a<0的解集为A,不等式x2-(3+a)x+2(1+a)≥0的解集为B.
(Ⅰ)当a=-4时,求A∪B;
(Ⅱ)若A∩B=A,求实数a的取值范围.
(Ⅰ)当a=-4时,求A∪B;
(Ⅱ)若A∩B=A,求实数a的取值范围.
考点:一元二次不等式的解法,并集及其运算,交集及其运算
专题:
分析:(I)由不等式2x-a<0可得解集A=(-∞,
).不等式x2-(3+a)x+2(1+a)≥0因式分解为(x-2)(x-1-a)≥0.
当a=-4时,A={x|x<-2},B={x|x≤-3或x≥2}.即可得出A∪B.
(II)由A∩B=A,可得A⊆B.对1+a与2的大小关系进行讨论即可得出.
| a |
| 2 |
当a=-4时,A={x|x<-2},B={x|x≤-3或x≥2}.即可得出A∪B.
(II)由A∩B=A,可得A⊆B.对1+a与2的大小关系进行讨论即可得出.
解答:
解:(I)由不等式2x-a<0解得x<
.∴解集A=(-∞,
).
不等式x2-(3+a)x+2(1+a)≥0化为(x-2)(x-1-a)≥0.
当a=-4时,A={x|x<-2},B={x|x≤-3或x≥2}.
∴A∪B={x|x<-2或x≥2}.
(II)∵A∩B=A,∴A⊆B.
∵A=(-∞,
).
当1+a>2时,即a>1时,B={x|x≤2或x≥1+a},
∴
≤2,解得a≤4.∴1<a≤4.
当1+a=2时,即a=1时,B=R.满足A⊆B,∴a=1.
当1+a<2时,即a<1时,B={x|x≤1+a或x≥2},
∵A⊆B,∴1+a≥
,解得a≥-1,∴-2≤a<1.
综上可得:-2≤a≤4.
| a |
| 2 |
| a |
| 2 |
不等式x2-(3+a)x+2(1+a)≥0化为(x-2)(x-1-a)≥0.
当a=-4时,A={x|x<-2},B={x|x≤-3或x≥2}.
∴A∪B={x|x<-2或x≥2}.
(II)∵A∩B=A,∴A⊆B.
∵A=(-∞,
| a |
| 2 |
当1+a>2时,即a>1时,B={x|x≤2或x≥1+a},
∴
| a |
| 2 |
当1+a=2时,即a=1时,B=R.满足A⊆B,∴a=1.
当1+a<2时,即a<1时,B={x|x≤1+a或x≥2},
∵A⊆B,∴1+a≥
| a |
| 2 |
综上可得:-2≤a≤4.
点评:本题考查了一元二次不等式的解法、集合的运算关系等基础知识,考查了分类讨论思想方法,属于难题.

练习册系列答案
相关题目
按流程图的程序计算,若开始输入的值为x=2,则输出的x的值是( )

| A、231 | B、156 |
| C、21 | D、15 |
若a>1,设函数f(x)=ax+x-2的零点为m,g(x)=logax+x-2的零点为n,则
+
的取值范围是( )
| 1 |
| m |
| 1 |
| n |
| A、(2,+∞) | ||
B、(
| ||
| C、(4,+∞) | ||
D、(
|
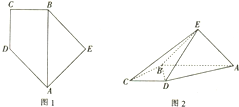 已知直角梯形ABCD的下底与等腰三角形ABE的斜边重合,AB⊥BC且AB=2CD=2BC(如图1),将此图形沿AB折叠成直二面角,连结EC、ED,得到四棱锥E-ABCD(如图2)
已知直角梯形ABCD的下底与等腰三角形ABE的斜边重合,AB⊥BC且AB=2CD=2BC(如图1),将此图形沿AB折叠成直二面角,连结EC、ED,得到四棱锥E-ABCD(如图2)