题目内容
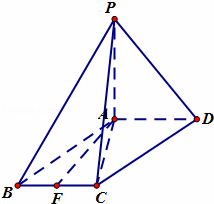
如图四棱锥P﹣ABCD中,底面ABCD是平行四边形,∠ACB=90°,PA⊥平面ABCD,F是BC的中点.
(1)求证:DA⊥平面PAC;
(2)试在线段PD上确定一点G,使CG∥平面PAF,并说明理由.
考点:
直线与平面垂直的判定;直线与平面平行的性质.
专题:
空间位置关系与距离.
分析:
(1)利用平行四边形的性质和平行线的性质可得AD⊥AC,再利用线面垂直的性质可得PA⊥AC,利用线面垂直的判定定理即可证明;
(2)设PD的中点为G,在平面PAD内作GH⊥PA于H,利用三角形的中位线定理可得GH![]()
![]() ,进而得到平行四边形CFGH,得到GC∥FH,利用线面平行的判定定理即可证明.
,进而得到平行四边形CFGH,得到GC∥FH,利用线面平行的判定定理即可证明.
解答:
(1)证明:∵四边形ABCD是平行四边形,
∴BC∥AD,
∴∠ACB=∠DAC=90°,∴DA⊥AC.
∵PA⊥平面ABCD,
∴PA⊥DA,又AC⊥DA,AC∩PA=A,
∴DA⊥平面PAC.
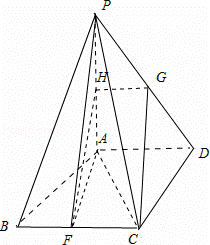
(Ⅱ)设PD的中点为G,在平面PAD内作GH⊥PA于H,则GH![]()
![]() ,
,
连接FH,则四边形FCGH为平行四边形,
∴GC∥FH,
∵FH⊂平面PAE,CG⊄平面PAE,
∴CG∥平面PAE,
∴G为PD中点时,CG∥平面PAE.
点评:
熟练掌握平行四边形的性质和平行线的性质、线面垂直的性质、判定定理、三角形的中位线定理、平行四边形判定与性质定理、线面平行的判定定理是解题的关键.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
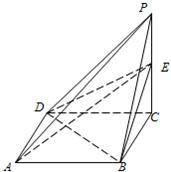 19、如图四棱锥P-ABCD,PC⊥面ABCD,PC=2,面ABCD是边长为1的正方形,E是侧棱PC上的动点.
19、如图四棱锥P-ABCD,PC⊥面ABCD,PC=2,面ABCD是边长为1的正方形,E是侧棱PC上的动点.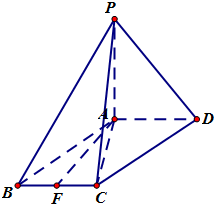 如图四棱锥P-ABCD中,底面ABCD是平行四边形,∠ACB=90°,PA⊥平面ABCD,F是BC的中点.
如图四棱锥P-ABCD中,底面ABCD是平行四边形,∠ACB=90°,PA⊥平面ABCD,F是BC的中点.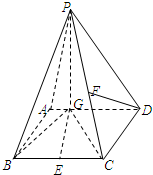 如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABCD,垂足为G,G在AD上,且PG=4,AG=
如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABCD,垂足为G,G在AD上,且PG=4,AG= 如图四棱锥P-ABCD中,底面ABCD是平行四边形,PC⊥平面ABCD,F是DC的中点,
如图四棱锥P-ABCD中,底面ABCD是平行四边形,PC⊥平面ABCD,F是DC的中点,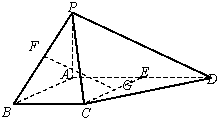 如图四棱锥P-ABCD中,ABCE为菱形,E、G、F分别是线段AD、CE、PB的中点.求证:FG∥平面PDC.
如图四棱锥P-ABCD中,ABCE为菱形,E、G、F分别是线段AD、CE、PB的中点.求证:FG∥平面PDC.