题目内容
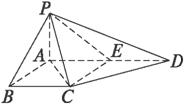
 如图四棱锥P-ABCD中,底面ABCD是平行四边形,PC⊥平面ABCD,F是DC的中点,
如图四棱锥P-ABCD中,底面ABCD是平行四边形,PC⊥平面ABCD,F是DC的中点,| AE |
| EP |
(Ⅰ)试判断直线EF与平面PBC的位置关系,并予以证明;
(Ⅱ)若四棱锥P-ABCD体积为
| 8 |
| 3 |
| 2 |
分析:(Ⅰ)直线EF与平面PBC相交,过E作EG∥AB交PB于G,根据题中条件可得:FC≠EG,又因为FC∥AB,所以EG∥FC,进而得到两条直线相交.,即可得到直线与平面相交.
(Ⅱ)过B作BH⊥CD于H,由四棱锥P-ABCD体积为
,结合题中的条件可得BH=
,所以CH=
,所以BH=CH=HD,所以DB⊥BC.再利用面面垂直的判定定理可得面面垂直.
(Ⅱ)过B作BH⊥CD于H,由四棱锥P-ABCD体积为
| 8 |
| 3 |
| 2 |
| 2 |
解答: 证明:(Ⅰ)直线EF与平面PBC相交.…(2分)
证明:(Ⅰ)直线EF与平面PBC相交.…(2分)
证明如下:过E作EG∥AB交PB于G,
∵
=2
,∴
=
,
∴EG=
AB,∵FC=
CD=
AB,
∴FC≠EG…(4分)
由底面ABCD是平行四边形得FC∥AB,
∴EG∥FC…(5分)
∴EF与CG相交,
故直线EF与平面PBC相交.…(6分)
(Ⅱ)解:过B作BH⊥CD于H,
∵四棱锥P-ABCD体积为
,PC⊥平面ABCD,
∴
PC•DC•BH=
,PC⊥BD.
∴BH=
,…(9分)
∵BC=2∴CH=
,
∵CD=2
,
∴BH=CH=HD,
∴DB⊥BC.
∴DB⊥面PBC,…(11分)
∵BD?面BDE,
∴平面BDE⊥面PBC.…(12分)
 证明:(Ⅰ)直线EF与平面PBC相交.…(2分)
证明:(Ⅰ)直线EF与平面PBC相交.…(2分)证明如下:过E作EG∥AB交PB于G,
∵
| AE |
| EP |
| PE |
| PA |
| 1 |
| 3 |
∴EG=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
∴FC≠EG…(4分)
由底面ABCD是平行四边形得FC∥AB,
∴EG∥FC…(5分)
∴EF与CG相交,
故直线EF与平面PBC相交.…(6分)
(Ⅱ)解:过B作BH⊥CD于H,
∵四棱锥P-ABCD体积为
| 8 |
| 3 |
∴
| 1 |
| 3 |
| 8 |
| 3 |
∴BH=
| 2 |
∵BC=2∴CH=
| 2 |
∵CD=2
| 2 |
∴BH=CH=HD,
∴DB⊥BC.
∴DB⊥面PBC,…(11分)
∵BD?面BDE,
∴平面BDE⊥面PBC.…(12分)
点评:本题考查线面的位置关系与面面垂直的判定定理,解决此类问题的关键是熟练掌握几何体的结构特征,以便利用有关定理进行证明与推理论证.

练习册系列答案
相关题目
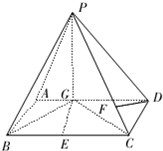 已知如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABC,垂足G在AD上,且
已知如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABC,垂足G在AD上,且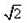 ,F是BC的中点.
,F是BC的中点.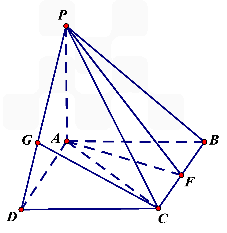
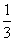 GD,GB⊥GC,GB=GC=2,PC=4,E是BC的中点.
GD,GB⊥GC,GB=GC=2,PC=4,E是BC的中点.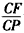 的值。
的值。 
 ,E是BC的中点.
,E是BC的中点. 的值.
的值.