题目内容
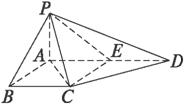
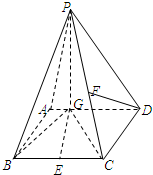 如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABCD,垂足为G,G在AD上,且PG=4,AG=
如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABCD,垂足为G,G在AD上,且PG=4,AG=| 1 |
| 3 |
(1)求异面直线GE与PC所成的角的余弦值;
(2)求点D到平面PBG的距离;
(3)若F点是棱PC上一点,且DF⊥GC,求
| PF |
| FC |
分析:(1)以G点为原点,GB,GC,GP为x轴、y轴、z轴建立空间直角坐标系,写出要用的点的坐标,写出两条异面直线对应的向量,根据两个向量的所成的角确定异面直线所成的角.
(2)计算点到面的距离,需要先做出面的法向量,在法向量与点到面的一个点所成的向量之间的运算,得到结果.
(3)设出点的坐标,根据两条线段垂直,得到两个向量的数量积等于0,解出点到坐标,根据向量的模长之比等于线段之比,得到结果.
(2)计算点到面的距离,需要先做出面的法向量,在法向量与点到面的一个点所成的向量之间的运算,得到结果.
(3)设出点的坐标,根据两条线段垂直,得到两个向量的数量积等于0,解出点到坐标,根据向量的模长之比等于线段之比,得到结果.
解答:解:(1)以G点为原点,GB,GC,GP为x轴、y轴、
z轴建立空间直角坐标系,则B(2,0,0),C(0,2,0),

P(0,0,4),故E(1,1,0)
=(1,1,0),
=(0,2,4).
cosθ=
=
,
∴GE与PC所成的余弦值为
(2)平面PBG的单位法向量
=(0,±1,0)
∵
=
=
=(-
,
,0),
∴点D到平面PBG的距离为|
•
|=
(3)设F(0,y,z),则
=(0,y,z)-(-
,
,0)=(
,y-
,z)
∵
⊥
,
∴(
,y-
,z)(0,20)=2y-3=0,
∴y=
,又
=λ
,即(0,
,z-4)=λ(0,2,-4),∴z=1,
故F(0,
,1),
=(0,
,-3),
=(0,
,-1),
∴
=
=3.
z轴建立空间直角坐标系,则B(2,0,0),C(0,2,0),

P(0,0,4),故E(1,1,0)
| GE |
| PC |
cosθ=
| ||||
|
|
| ||
| 10 |
∴GE与PC所成的余弦值为
| ||
| 10 |
(2)平面PBG的单位法向量
| n |
∵
| GD |
| 3 |
| 4 |
| AD |
| 3 |
| 4 |
| BC |
| 3 |
| 2 |
| 3 |
| 2 |
∴点D到平面PBG的距离为|
| GD |
| n |
| 3 |
| 2 |
(3)设F(0,y,z),则
| DF |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
∵
| DF |
| GC |
∴(
| 3 |
| 2 |
| 3 |
| 2 |
∴y=
| 3 |
| 2 |
| PF |
| PC |
| 3 |
| 2 |
故F(0,
| 3 |
| 2 |
| PF |
| 3 |
| 2 |
| FC |
| 1 |
| 2 |
∴
| PF |
| FC |
| ||||
|
点评:本题考查空间几何量的计算,准确把握立体几何的最新发展趋势:这样可以减低题目的难度,坚持向量法与公理化法的“双轨”处理模式,在复习备考时应引起高度注意.

练习册系列答案
相关题目
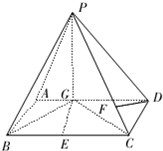 已知如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABC,垂足G在AD上,且
已知如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABC,垂足G在AD上,且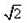 ,F是BC的中点.
,F是BC的中点.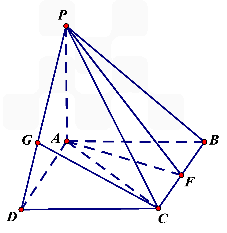
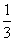 GD,GB⊥GC,GB=GC=2,PC=4,E是BC的中点.
GD,GB⊥GC,GB=GC=2,PC=4,E是BC的中点.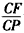 的值。
的值。 
 ,E是BC的中点.
,E是BC的中点. 的值.
的值.