题目内容

2．已知函数f（x）=x+2x，g（x）=x+lnx，$h（x）=x-\sqrt{x}-1$的零点分别为x1，x2，x3，则x1，x2，x3的大小关系是（　　）
A．x2＜x1＜x3B．x1＜x2＜x3C．x1＜x3＜x2D．x2＜x3＜x1

分析 由函数f（x）=x+2x，g（x）=x+lnx，$h（x）=x-\sqrt{x}-1$的零点分别为x1，x2，x3，即函数令y1=2x，y2=lnx，y=-$\sqrt{x}$-1与函数y=-x的交点的横坐标分别为x1，x2，x3，作出函数的图象，结合函数的图象可判断

解答 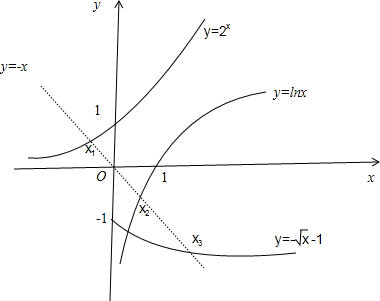解：由函数f（x）=x+2x，g（x）=x+lnx，$h（x）=x-\sqrt{x}-1$的零点分别为x1，x2，x3，
即函数令y1=2x，y2=lnx，y=-$\sqrt{x}$-1与函数y=-x的交点的横坐标分别为x1，x2，x3，
作出函数的图象，结合图象可得x1＜x2＜x3，
故选：B．

点评 本题主要考查了方程的零点的大小的判断，解题的关键是结合函数的图象，体现了方程与函数的相互转换及数形结合的数学思想的应用．属于难题．

练习册系列答案
相关题目
12．设矩阵A=$[\begin{array}{l}{m}&{0}\\{0}&{n}\end{array}]$，若矩阵A的属于特征值1的一个特征向量为$[\begin{array}{l}{1}\\{0}\end{array}]$，属于特征值2的一个特征向量为$[\begin{array}{l}{0}\\{1}\end{array}]$，求矩阵A．
13．已知i是虚数单位，若复数z=-i（a+i）（a∈R）的实部与虚部相等，则z的共轭复数${\;}_{z}^{-}$=（　　）
A．-1+iB．1+iC．1-iD．-1-i
10．能反映样本数据的离散程度大小的数字特征是（　　）
A．众数B．平均数C．中位数D．标准差
17．已知图1是一个边长为1的正三角形，三边中点的连线将它分成四个小三角形，去掉中间的一个小三角形，得到图2，再对图2中剩下的三个小三角形重复前述操作，得到图3，重复这种操作可以得到一系列图形．记第n个图形中所有剩下的小三角形的面积之和为an，所以去掉的三角形的周长之和为bn．
（ I） 试求a4，b4；
（ II） 试求an，bn．
7．如图，菱形ABCD中，∠A=60°，沿BD折成直二面角A-BD-C，过点A作PA⊥平面ABD，连接AC、PC、PD．
（Ⅰ）求证：PA∥平面BCD；
（Ⅱ）求二面角A-BC-D的余弦值．
14．甲、乙、丙、丁、戊五名同学站成一排，甲不站两端且不与乙相邻的排法数是（　　）
A．24B．12C．48D．36
11．已知甲、乙、丙、丁四人排成一行，甲和乙相邻，甲和丙不相邻，则不同的排法有8种．（用数字作答）
7．设a，b为非零实数，且a＜b，则下列不等式恒成立的是（　　）
A．a-b＞0B．a2＜b2C．$\frac{1}{a{b}^{2}}$$＜\frac{1}{{a}^{2}b}$D．$\frac{1}{{b}^{2}}$$＜\frac{1}{{a}^{2}}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网