题目内容
若集合A={（x，y）|y=1+
}，B={（x，y）|y=k（x-2）+4}，当集合A∩B有4个子集时，实数k的取值范围是 ．
| 4-x2 |
考点：子集与真子集
专题：函数的性质及应用,集合
分析：若集合A∩B有4个子集，则集合A∩B有2个元素，即函数y=1+
和y=k（x-2）+4有两个交点，在同一坐标系中画出函数y=1+
和y=k（x-2）+4的图象，数形结合可得答案．
| 4-x2 |
| 4-x2 |
解答：
解：若集合A∩B有4个子集，则集合A∩B有2个元素，
即函数y=1+
和y=k（x-2）+4有两个交点，
在同一坐标系中画出函数y=1+
和y=k（x-2）+4的图象如下图所示：
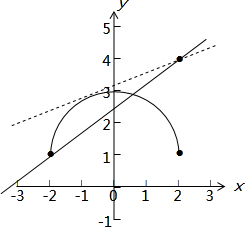
由图可知：当
＜k≤
时，满足条件，
故实数k的取值范围是（
，
]，
故答案为：（
，
]
即函数y=1+
| 4-x2 |
在同一坐标系中画出函数y=1+
| 4-x2 |
由图可知：当
| 5 |
| 12 |
| 3 |
| 4 |
故实数k的取值范围是（
| 5 |
| 12 |
| 3 |
| 4 |
故答案为：（
| 5 |
| 12 |
| 3 |
| 4 |
点评：本题考查的知识点是子集与真子集，直线与圆的位置关系，其中分析出函数y=1+
和y=k（x-2）+4有两个交点，是解答的关键．
| 4-x2 |
练习册系列答案
相关题目
利用随机模拟方法计算如图阴影部分（y=1和y=x2所围成的部分）的面积S时，若向矩形ABCD内随机撒1000粒豆子，落在阴影区域内的有698粒，由此可得S的近似值为