题目内容
当x∈（1，2）时，不等式x2+mx+4＜0恒成立，则m的取值范围为（ ）
| A、（-∞，-5） |
| B、（-∞，-5] |
| C、（-5，+∞） |
| D、[-5，+∞） |
考点：一元二次不等式的解法
专题：不等式的解法及应用
分析：先构造函数f（x）=x2+mx+4，根据零点存在定理的应用，得到关于m的不等式组，解得即可
解答：
解：根据题意，构造函数：f（x）=x2+mx+4，x∈[1，2]．由于当x∈（1，2）时，不等式x2+mx+4＜0恒成立，
即
，即
解得 m≤-5
所以m的取值范围为（-∞，-5]，
故选B．
即
|
|
解得 m≤-5
所以m的取值范围为（-∞，-5]，
故选B．
点评：本题考查函数恒成立问题，考查构造函数思想与运算求解能力，属于中档题．
练习册系列答案
培优好卷单元加期末卷系列答案
一线名师权威作业本系列答案
相关题目
集合A={a，b}，B={-1，0，1}，从A到B的映射f满足f（a）+f（b）=0，那么这样的映射f的个数有（ ）
| A、2个 | B、3个 | C、5个 | D、8个 |
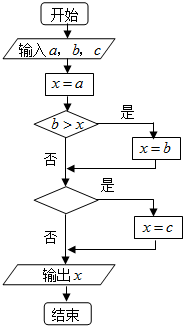如图的程序框图，如果输入三个实数a，b，c，要求输出这三个数中最大的数，那么在空白的判断框中，应该填入下面四个选项中的（ ）| A、c＞x | B、x＞a |
| C、c＞b | D、b＞c |