题目内容
6.已知函数f(x)=|2x+a|,a∈R.(Ⅰ)当a=-1时,求不等式f(x)+|x+1|-3≤0的解集;
(Ⅱ)若对?x∈[1,2],f(x)<x2+1恒成立,求a的取值范围.
分析 (Ⅰ)当a=-1时,不等式f(x)+|x+1|-3≤0,即为不等式|2x-1+|x+1|-3≤0,分类讨论求不等式f(x)+|x+1|-3≤0的解集;
(Ⅱ)若对?x∈[1,2],f(x)<x2+1恒成立,即?x∈[1,2],|2x+a|<x2+1恒成立,分离参数求最值,即可求a的取值范围.
解答 解:(Ⅰ) 当a=-1时,不等式f(x)+|x+1|-3≤0,即为不等式|2x-1+|x+1|-3≤0.
∴$\left\{\begin{array}{l}{x<-1}\\{-3x-3≤0}\end{array}\right.$或$\left\{\begin{array}{l}{-1≤x≤\frac{1}{2}}\\{-x-1≤0}\end{array}\right.$或$\left\{\begin{array}{l}{x>\frac{1}{2}}\\{3x-3≤0}\end{array}\right.$,
解得:x∈∅或-1≤x≤$\frac{1}{2}$或$\frac{1}{2}$<x≤1.
∴不等式|2x-1+|x+1|-3≤0的解集为[-1,1].…(5分)
(Ⅱ)?x∈[1,2],f(x)<x2+1恒成立,即?x∈[1,2],|2x+a|<x2+1恒成立,
而-x2-1<2x+a<x2+1,
∴?x∈[1,2],-x2-2x-1<a<x2-2x+1,恒成立,
设g(x)=-x2-2x-1,h(x)=x2-2x+1,
可转化为∴?x∈[1,2],g(x)max<a<h(x)min,
∴-4<a<0,∴a的取值范围是(-4,0).…(10分)
点评 本题考查绝对值不等式的解法,考查恒成立问题,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
17.(x-y)(x+y)8的展开式中x2y7的系数是( )
| A. | -20 | B. | 20 | C. | -22 | D. | 22 |
14.由变量x与y相对应的一组数据(3,y1),(5,y2),(7,y3),(12,y4),(13,y5)得到的线性回归方程为$\stackrel{∧}{y}$=$\frac{1}{2}$x+20,则$\sum_{i=1}^{5}{y}_{i}$=( )
| A. | 25 | B. | 125 | C. | 120 | D. | 24 |
10.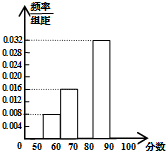 为了让学生了解环保知识,增强环保意识,某中学举行了一次环保知识竞赛,共有900名学生参加了这次竞赛.为了了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面尚未完成的频率分布表和频率分布直方图,解答下列问题:
为了让学生了解环保知识,增强环保意识,某中学举行了一次环保知识竞赛,共有900名学生参加了这次竞赛.为了了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面尚未完成的频率分布表和频率分布直方图,解答下列问题:
(Ⅰ)补全频率分布直方图;
(Ⅱ)根据频率分布直方图计算学生成绩的平均值.
 为了让学生了解环保知识,增强环保意识,某中学举行了一次环保知识竞赛,共有900名学生参加了这次竞赛.为了了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面尚未完成的频率分布表和频率分布直方图,解答下列问题:
为了让学生了解环保知识,增强环保意识,某中学举行了一次环保知识竞赛,共有900名学生参加了这次竞赛.为了了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面尚未完成的频率分布表和频率分布直方图,解答下列问题:(Ⅰ)补全频率分布直方图;
| 分组 | 频数 | 频率 |
| [50,60) | 4 | 0.08 |
| [60,70) | 8 | 0.16 |
| [70,80) | 10 | 0.20 |
| [80,90) | 16 | 0.32 |
| [90,100] | 12 | 0.24 |
| 合计 | 50 | 1 |
7.已知双曲线$\frac{{y}^{2}}{4}$-$\frac{{x}^{2}}{a}$=1的渐近线方程为y=±$\frac{2\sqrt{3}}{3}$x,则此双曲线的离心率是( )
| A. | $\frac{\sqrt{7}}{2}$ | B. | $\frac{\sqrt{13}}{3}$ | C. | $\frac{5}{3}$ | D. | $\frac{\sqrt{21}}{3}$ |