题目内容
4．已知角θ的终边经过点P（-x，-6），且cosθ=-$\frac{3}{5}$，则x=（ ）| A． | $\frac{9}{2}$ | B． | -$\frac{9}{2}$ | C． | $\frac{2}{9}$ | D． | -$\frac{2}{9}$ |
分析 根据题意，由点P的坐标可得r=|OP|的值，由三角函数余弦的定义可得cosθ=$\frac{-x}{\sqrt{{x}^{2}+36}}$=-$\frac{3}{5}$，解可得x的值，即可得答案．
解答 解：根据题意，角θ的终边经过点P（-x，-6），
则r=|OP|=$\sqrt{（-x）^{2}+{6}^{2}}$=$\sqrt{{x}^{2}+36}$，
则cosθ=$\frac{-x}{\sqrt{{x}^{2}+36}}$=-$\frac{3}{5}$，
解可得x=$\frac{9}{2}$；
故选：A．
点评 本题考查任意角三角函数的定义，关键是牢记任意角三角函数的定义并熟练运用．
练习册系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
15．已知定义在R上的函数f（x）满足f（x）+$\frac{1}{2}cos2x$在（0，+∞）上是减函数，且?x∈R，有f（-x）+f（x）=2sin2x，则以下大小关系一定正确的是（ ）
| A． | f（$\frac{5π}{6}$）＜f（$\frac{4π}{3}$） | B． | f（$\frac{π}{4}$）＜f（π） | C． | f（-$\frac{5π}{6}$）＜f（-$\frac{4π}{3}$） | D． | f（-$\frac{π}{4}$）＜f（-π） |
19．一辆汽车在司机猛踩刹车后5s内停下．在这一刹车过程中，下面各速度值被记录了下来：
求刹车踩下后汽车滑过的距离的不足近似值（每个ξi均取为小区间的右端点）与过剩近似值（每个ξi均取为小区间的左端点）．
| 刹车踩下后的时间/s | 0 | 1 | 2 | 3 | 4 | 5 |
| 速度/（m•s-1） | 27 | 18 | 12 | 7 | 3 | 0 |
13．（x-y）（x+y）5展开式中，x4y2的系数为（ ）
| A． | 5 | B． | -5 | C． | 10 | D． | -10 |
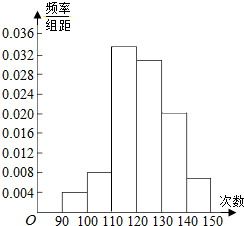为了了解高一学生的体能情况，某校抽取部分学生进行一部分跳绳次数测试，将所得数据整理后，画出频率分布直方图（如图所示），图中从左到右各小长方形面积之比为2：4：17：15：9：3，第二小组频数为12，若次数在110以上（含110次）为达标，试估计该学校全体高一学生单调达标率是0.88．