题目内容
14．若函数f（x）=3ax-k+1（a＞0，且a≠1）过定点（2，4），且f（x）在定义域R内是增函数，则函数g（x）=loga（x-k）的图象是（ ）| A． |  | B． |  | C． |  | D． |  |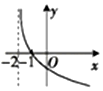
分析 根据指数函数的单调性确定a的范围以及k的值，结合对数函数的单调性和图象关系进行判断即可．
解答 解：由题意可知f（2）=4，3a2-k+1=4解得k=2，
所以f（x）=ax-2+1，
又因为是减函数，
所以0＜a＜1．
此时g（x）=loga（x-2）也是单调减的，且过点（3，0）．故选A符合题意．
故选：A．
点评 本题主要考查指数函数和对数函数图象的应用，结合函数单调性的性质是解决本题的关键．
练习册系列答案
举一反三同步巧讲精练系列答案
口算与应用题卡系列答案
相关题目
2．已知x，y满足$\left\{\begin{array}{l}{x-y≥0}\\{x+y-4≥0}\\{x≤4}\end{array}\right.$，则z=4x+y的最小值为（ ）
| A． | 6 | B． | 8 | C． | 10 | D． | 15 |
9．已知sinα=$\frac{3}{5}$，cosα=$\frac{4}{5}$，则sin2α=（ ）
| A． | $\frac{7}{5}$ | B． | $\frac{12}{5}$ | C． | $\frac{12}{25}$ | D． | $\frac{24}{25}$ |
19．在△ABC中tanA+tanB=1-tanAtanB则∠A+∠B等于（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{4}$ | C． | $\frac{π}{3}$ | D． | $\frac{π}{2}$ |
6．已知函数f（x）满足f（-x）=f（x）和f（x+2）=f（x），且当x∈[0，1]时，f（x）=1-x，则函数g（x）=f（x）-（$\frac{1}{3}$）x在x∈[-4，4]上零点的个数是（ ）
| A． | 5 | B． | 4 | C． | 3 | D． | 2 |
4．已知$\overrightarrow a=（cos{66°}，sin{6°}），\overrightarrow b=（cos{6°}，sin{66°}），则\overrightarrow a•\overrightarrow b$等于（ ）
| A． | $-\frac{1}{2}$ | B． | $\frac{1}{2}$ | C． | $-\frac{{\sqrt{3}}}{2}$ | D． | $\frac{{\sqrt{3}}}{2}$ |