题目内容
(本小题满分14分)
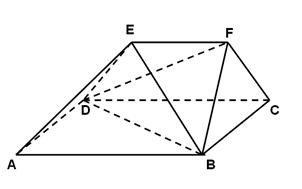
如图所示,在四面体P—ABC中,已知PA=BC=6,PC=AB=8,AC=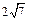 ,PB=10,F是线段PB上一点,
,PB=10,F是线段PB上一点,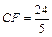 ,点E在线段AB上,且EF⊥PB.
,点E在线段AB上,且EF⊥PB.
(Ⅰ)证明:PB⊥平面CEF;
(Ⅱ)求二面角B—CE—F的正弦值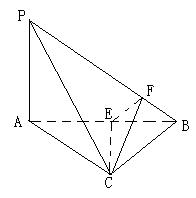
如图所示,在四面体P—ABC中,已知PA=BC=6,PC=AB=8,AC=
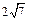 ,PB=10,F是线段PB上一点,
,PB=10,F是线段PB上一点,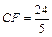 ,点E在线段AB上,且EF⊥PB.
,点E在线段AB上,且EF⊥PB.(Ⅰ)证明:PB⊥平面CEF;
(Ⅱ)求二面角B—CE—F的正弦值

(Ⅰ)略
(Ⅱ)二面角B—CE—F的正弦值是
(Ⅱ)二面角B—CE—F的正弦值是

(I)证明:∵
∴ ……2分
……2分
∴ PB边上的高= ,……4分
,……4分
又∵ , ∴
, ∴ ……6分
……6分
又EF⊥PB , ∴ PB⊥平面CEF ……8分
(2)∵PB⊥平面CEF且 平面CEF ∴
平面CEF ∴
∵ ∴
∴
又∵ , ∴
, ∴ , ∵
, ∵
∴PA⊥平面ABC,由 平面ABC, ∴
平面ABC, ∴
∵ , ∴
, ∴ 平面
平面 ……11分
……11分
∴ 平面PAB, ∴
平面PAB, ∴ ,
, ,故∠FEB是二面角B—CE—F的平面角
,故∠FEB是二面角B—CE—F的平面角 ……12分
……12分
∵EF⊥PB, PB⊥AB ∴ ……14分
……14分
二面角B—CE—F的正弦值是

∴
 ……2分
……2分∴ PB边上的高=
 ,……4分
,……4分又∵
 , ∴
, ∴ ……6分
……6分又EF⊥PB , ∴ PB⊥平面CEF ……8分
(2)∵PB⊥平面CEF且
 平面CEF ∴
平面CEF ∴
∵
 ∴
∴
又∵
 , ∴
, ∴ , ∵
, ∵
∴PA⊥平面ABC,由
 平面ABC, ∴
平面ABC, ∴
∵
 , ∴
, ∴ 平面
平面 ……11分
……11分∴
 平面PAB, ∴
平面PAB, ∴ ,
, ,故∠FEB是二面角B—CE—F的平面角
,故∠FEB是二面角B—CE—F的平面角 ……12分
……12分∵EF⊥PB, PB⊥AB ∴
 ……14分
……14分二面角B—CE—F的正弦值是


练习册系列答案
相关题目
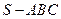 中,
中,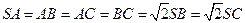 ,
,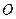 为
为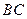 的中点.
的中点.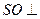 面
面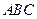 ;
;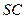 与
与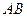 所成角的余弦值.
所成角的余弦值.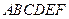 中,四边形
中,四边形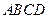 是正方形,
是正方形,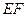 ∥
∥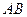 ,
,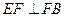 ,
,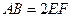 ,
,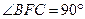 ,
,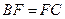 .
.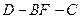 的正切值;
的正切值;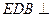 平面
平面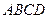 .
.
 边长为2的菱形,
边长为2的菱形,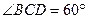 ,E是CD的中点,PA
,E是CD的中点,PA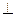 底面ABC
底面ABC D,PA=4
D,PA=4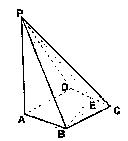
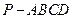 中,底面
中,底面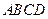 是边长为
是边长为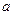 的正方形,侧面
的正方形,侧面 ,且
,且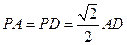 ,若
,若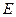 、
、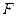 分别为
分别为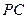 、
、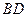 的中点.
的中点.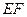 ∥平面
∥平面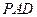 ;
;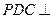 平面
平面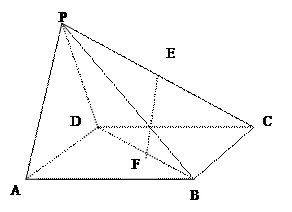
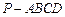 中,底面
中,底面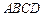 是菱形,
是菱形,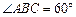 ,
,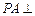 平面
平面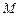 、
、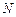 分别为
分别为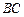 、
、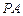 的中点,
的中点,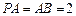 .
.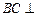 平面
平面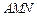 ;
;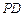 上是否存在一点
上是否存在一点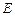 ,使得
,使得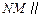 平面
平面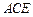 ;若存在,
;若存在, 求出
求出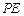 的长;若不存在,请说明理由。
的长;若不存在,请说明理由。
 ,平面
,平面 ,下列命题正确的是( )
,下列命题正确的是( ) ,
, ,且
,且 ,则
,则
 .
. ,
, ,则
,则 .
. ,则
,则 ,则
,则 .
. 行
行 是两条直线,
是两条直线, 是两个
是两个 平面,则下列命题中错误的是 ( )
平面,则下列命题中错误的是 ( )


