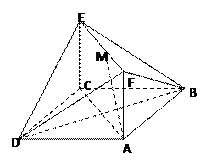题目内容
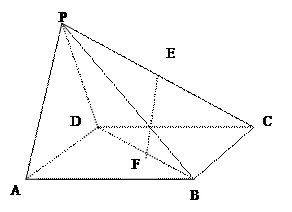
(8分) 如图,在四棱锥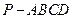 中,底面
中,底面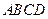 是边长为
是边长为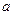 的正方形,侧面
的正方形,侧面 ,且
,且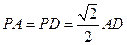 ,若
,若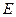 、
、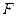 分别为
分别为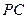 、
、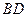 的中点.
的中点.
(1)求证: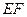 ∥平面
∥平面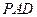 ;
;
(2)求证:平面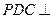 平面
平面 .
.
 中,底面
中,底面 是边长为
是边长为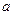 的正方形,侧面
的正方形,侧面 ,且
,且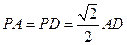 ,若
,若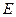 、
、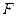 分别为
分别为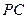 、
、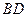 的中点.
的中点.(1)求证:
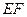 ∥平面
∥平面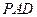 ;
;(2)求证:平面
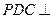 平面
平面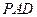 .
.
略
证明:(1)连结AC,则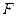 是
是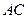 的中点,在△
的中点,在△ 中,EF∥PA,
中,EF∥PA,
且PA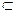 平面PAD,EF
平面PAD,EF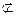 平面PAD,
平面PAD,
∴EF∥平面PAD
证明:(2)因为平面PAD⊥平面ABCD, 平面PAD∩平面ABCD=AD,
又CD⊥AD,所以,CD⊥平面PAD,∴CD⊥PA
又PA=PD=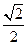 AD,所以△PAD是等腰直角三角形,
AD,所以△PAD是等腰直角三角形,
且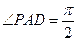 ,即PA⊥PD
,即PA⊥PD
又CD∩PD=D, ∴ PA ⊥平面PDC,
⊥平面PDC,
又PA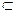 平面PAD,
平面PAD,
所以 平面PAD⊥平面PDC
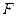 是
是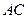 的中点,在△
的中点,在△ 中,EF∥PA,
中,EF∥PA, 且PA
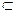 平面PAD,EF
平面PAD,EF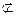 平面PAD,
平面PAD,∴EF∥平面PAD
证明:(2)因为平面PAD⊥平面ABCD, 平面PAD∩平面ABCD=AD,
又CD⊥AD,所以,CD⊥平面PAD,∴CD⊥PA
又PA=PD=
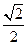 AD,所以△PAD是等腰直角三角形,
AD,所以△PAD是等腰直角三角形,且
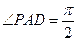 ,即PA⊥PD
,即PA⊥PD 又CD∩PD=D, ∴ PA
 ⊥平面PDC,
⊥平面PDC,又PA
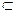 平面PAD,
平面PAD,所以 平面PAD⊥平面PDC

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
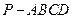 中,底面
中,底面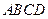 是矩形,
是矩形,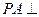 平面
平面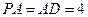 ,
,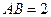 . 以
. 以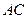 的中点
的中点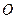 为球心、
为球心、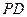 于点
于点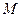 ,交
,交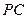 于点
于点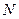 .
.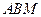 ⊥平面
⊥平面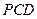 ;
;
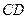 与平面
与平面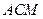 所成的角的正弦值.
所成的角的正弦值.
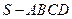 的底面是正方形,每条侧棱长都是底面边长的
的底面是正方形,每条侧棱长都是底面边长的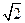 倍,P为侧棱SD上的点。
倍,P为侧棱SD上的点。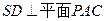 ,求二面角
,求二面角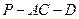 的大小;
的大小;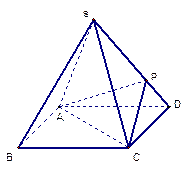
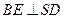 ,若存在,求
,若存在,求 的值;若不存在,试说明理由。
的值;若不存在,试说明理由。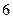 的正方体
的正方体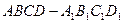 中,
中,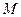 是
是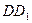 的中点,
的中点,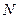 在线段
在线段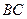 上,且
上,且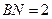 .
.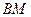 与
与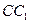 所成角的余弦值;
所成角的余弦值;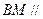 面
面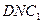 ;
;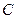 到面
到面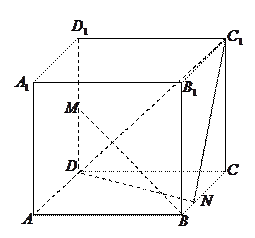
 ,PB=10,F是线段PB上一点,
,PB=10,F是线段PB上一点,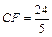 ,点E在线段AB上,且EF⊥PB.
,点E在线段AB上,且EF⊥PB.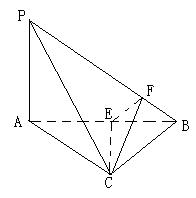
 为矩形,
为矩形,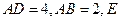 、
、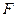 分别是线段
分别是线段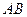 、
、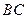 的中点,
的中点,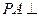 平面
平面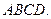 (1)求证:
(1)求证: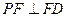 ;
;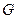 在
在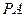 上,且
上,且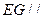 平面
平面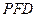 ,试确定点
,试确定点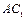 中,
中, 为棱
为棱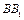 的中点,则在平面
的中点,则在平面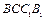 内过点
内过点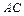 成
成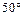 角的直线有( )
角的直线有( )
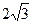 AF,且点M是线段EF的中点.
AF,且点M是线段EF的中点.