题目内容
4.已知数列{an}中,an=$\frac{1}{(n+1)^{2}}$,记f(n)=(1-a1)(1-a2)…(1-an),试计算f(1),f(2),f(3)的值,推测f(n)的表达式为f(n)=$\frac{n+2}{2(n+1)}$.分析 根据f(n)=(1-a1)(1-a2)…(1-an),依次求得f(1),f(2),f(3)的值,将结果转化为同一的结构形式,进而推广到一般得出f(n)的值.
解答 解:∵f(n)=(1-a1)(1-a2)…(1-an),an=$\frac{1}{(n+1)^{2}}$,
∴f(1)=$\frac{3}{4}$,f(2)=$\frac{3}{4}•\frac{8}{9}$=$\frac{4}{6}$,f(3)=$\frac{2}{3}•\frac{15}{16}$=$\frac{5}{8}$,…,
根据其结构特点可得:f(n)=$\frac{n+2}{2(n+1)}$.
故答案为:$\frac{n+2}{2(n+1)}$.
点评 本题主要通过求值,来考查数列的规律性,同时还考查学生概括,抽象,推理,从具体到一般的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.抛物线y2=12x上与焦点的距离等于9的点的坐标是( )
| A. | $(6,6\sqrt{2})$或$(6,-6\sqrt{2})$ | B. | $(4,4\sqrt{3})$或$(4,-4\sqrt{3})$ | C. | (3,6)或(3,-6) | D. | $(9,6\sqrt{3})$或$(9,-6\sqrt{3})$ |
14.若α∈(0,π),且3cos2α=sin($\frac{π}{4}$-α),则sin2α的值为( )
| A. | 1或-$\frac{17}{18}$ | B. | $\frac{17}{18}$ | C. | 1 | D. | $-\frac{17}{18}$ |
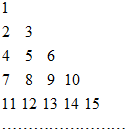 将全体正整数排成一个三角形数阵:按照以上的排列规律,第20行第2个数是192.
将全体正整数排成一个三角形数阵:按照以上的排列规律,第20行第2个数是192.