将全体正整数排成一个三角形数阵:按照以上的排列规律.第20行第2个数是192．题目和参考答案——青夏教育精英家教网——

题目内容

16．

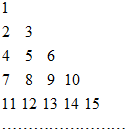将全体正整数排成一个三角形数阵：按照以上的排列规律，第20行第2个数是192．

分析前n-1行共有正整数1+2+…+（n-1）个，由此能求出第20行第2个数．

解答解：前n-1行共有正整数1+2+…+（n-1）个，
即$\frac{n（n-1）}{2}$=$\frac{{n}^{2}-n}{2}$个，
因此第20行第3个数是全体正整数中第$\frac{2{0}^{2}-20}{2}$+2=192个，
∴第20行第2个数是192．
故答案为：192．

点评本小题考查归纳推理和等差数列求和公式，是基础题，解题时要认真审题，注意等差数列的性质的合理运用．

练习册系列答案

名校课堂系列答案

西城学科专项测试系列答案

小考必做系列答案

小考实战系列答案

小考复习精要系列答案

小考总动员系列答案

小升初必备冲刺48天系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

相关题目

6．2³⁰⁰⁰的末两位数是（　　）

7．已知函数f（x）=$\frac{1}{3}$x³-$\frac{1}{2}$ax²-3x，且f（x）在x=-1处取得极值．
（Ⅰ）求a的值；
（Ⅱ）求f（x）在[0，5]上的最值．

4．已知数列{a_n}中，a_n=$\frac{1}{（n+1）^{2}}$，记f（n）=（1-a₁）（1-a₂）…（1-a_n），试计算f（1），f（2），f（3）的值，推测f（n）的表达式为f（n）=$\frac{n+2}{2（n+1）}$．

11．在吸烟与患肺病这两个分类变量的计算中，下列说法正确的是（　　）

	A．	若K²的观测值为k=6.635，我们有99%的把握认为吸烟与患肺病有关系，那么在100个吸烟的人中必有99人患有肺病
	B．	若从统计量中求出有95%的把握认为吸烟与患肺病有关系，是指有5%的可能性使得推断出现错误
	C．	从独立性检验可知有99%的把握认为吸烟与患肺病有关系时，我们说某人吸烟，那么他有99%的可能患有肺病
	D．	以上三种说法都不正确

1．已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的离心率e=$\frac{1}{2}$，且点$（1，\frac{3}{2}）$在椭圆上，
（1）求椭圆C的方程；
（2）已知A为椭圆C的左顶点，直线l过右焦点F₂与椭圆C交于M，N两点，若AM，AN的斜率k₁，k₂满足k₁+k₂=-1，求直线l的方程．

8．已知实数x、y、z满足x²+2y²+3z²=4，设T=xy+yz，则T的取值范围是（　　）

[$-\frac{\sqrt{6}}{3}$，$\frac{\sqrt{6}}{3}$]

[$-\frac{\sqrt{6}}{6}$，$\frac{2\sqrt{6}}{3}$]

[$-\frac{\sqrt{6}}{3}$，$\frac{\sqrt{3}}{3}$]

[$-\frac{2\sqrt{6}}{3}$，$\frac{2\sqrt{6}}{3}$]

5．对于集合{a₁，a₂，…，a_n}和常数a₀，定义：w=$\frac{sin（{a}_{1}-{a}_{0}）^{2}+sin（{a}_{2}-{a}_{0}）^{2}+…+sin（{a}_{n}-{a}_{0}）^{2}}{n}$为集合{a₁，a₂，…，a_n}相对于a₀的“正弦方差”，则集合{$\frac{π}{2}$，$\frac{5π}{6}$，$\frac{7π}{6}$}相对a₀的“正弦方差”为（　　）

$\frac{{a}_{0}}{4}$

$\frac{{a}_{0}}{3}$

6．以下四个命题中，真命题的个数是（　　）
①“若a+b≥2，则a，b中至少有一个不小于1”的逆命题
②?α₀，β₀∈R，使得sin（α₀+β₀）=sinα₀+sinβ₀
③若a∈R，则“$\frac{1}{a}$＜1”是“a＞1”的必要不充分条件²⁴
④命题“?x₀∈R，x₀²+2x₀+3＜0”的否定是“?x∈R，x²+2x+3＞0”