题目内容
9.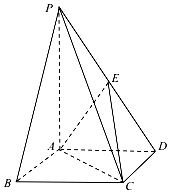 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PA⊥底面ABCD,点E是PD的中点,AB=2,PA=3.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PA⊥底面ABCD,点E是PD的中点,AB=2,PA=3.(1)求证:PB∥平面EAC;
(2)求证:CD⊥AE;
(3)求二面角E-AC-D的余弦值.
分析 (1)以A为坐标原点,AB、AD、AP所在的直线分别为x轴、y轴、z轴建立空间直角坐标系,利用向量法能证明PB∥平面EAC.
(2)求出$\overrightarrow{CD}=(-2,0,0),\overrightarrow{AE}=(0,1,\frac{3}{2})$,利用向量法能证明CD⊥AE.
(3)求出平面CAD的法向量和平面EAC的法向量,利用向量法能求出二面角C-PD-A的余弦值.
解答 证明:(1)如图,由已知得AB、AD、AP两两垂直,
以A为坐标原点,AB、AD、AP所在的直线分别为x轴、y轴、z轴建立空间直角坐标系,
则A(0,0,0),B(2,0,0),C(2,2,0),D(0,2,0),P(0,0,3),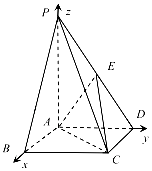
∵点E是PD的中点,∴点E的坐标为$E(0,1,\frac{3}{2})$,
∴$\overrightarrow{AC}=(2,2,0),\overrightarrow{AE}=(0,1,\frac{3}{2})$.
设平面EAC的法向量为$\overrightarrow n=(x,y,z)$,
由$\left\{{\begin{array}{l}{\overrightarrow n•\overrightarrow{AC}=0}\\{\overrightarrow n•\overrightarrow{AE}=0}\end{array}}\right.$,得$\left\{{\begin{array}{l}{x+y=0}\\{y+\frac{3}{2}z=0}\end{array}}\right.$,令x=1,得$\overrightarrow n=(1,-1,\frac{2}{3})$,
又$\overrightarrow{BP}=(-2,0,3)$,
∴$\overrightarrow{BP}•\overrightarrow n=-2+0+2=0$,∴$\overrightarrow{BP}⊥\overrightarrow n$,
∵PB?平面EAC,∴PB∥平面EAC.
(2)∵$\overrightarrow{CD}=(-2,0,0),\overrightarrow{AE}=(0,1,\frac{3}{2})$,
∴$\overrightarrow{CD}•\overrightarrow{AE}=-2×0+0×1+0×\frac{3}{2}=0$,
∴CD⊥AE.
解:(3)∵平面CAD的法向量为$\overrightarrow m=(0,0,3)$,
平面EAC的法向量为$\overrightarrow n=(1,-1,\frac{2}{3})$,
∴$cos<\overrightarrow m,\overrightarrow n>=\frac{\overrightarrow m•\overrightarrow n}{{|{\overrightarrow m}||{\overrightarrow n}|}}=\frac{2}{{3×\sqrt{1+1+\frac{4}{9}}}}=\frac{{\sqrt{22}}}{11}$,
由图形知二面角C-PD-A的平面是锐角,
∴二面角C-PD-A的余弦值为$\frac{{\sqrt{22}}}{11}$.
点评 本题考查线面平行的证明,考查线线垂直的证明,考查二面角的余弦值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

 ,则
,则 ( )
( ) B.
B. C.
C. D.
D.
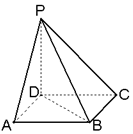 如图,已知ABCD是正方形,PD⊥平面ABCD,PD=AD.
如图,已知ABCD是正方形,PD⊥平面ABCD,PD=AD. 如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,PB⊥BC,PD⊥DC,且$PC=\sqrt{3}$.
如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,PB⊥BC,PD⊥DC,且$PC=\sqrt{3}$.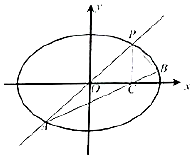 如图所示,已知椭圆$E:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$过点$({\sqrt{2},\sqrt{2}})$,直线l:y=kx(k≠0)与椭圆E交于P、A两点,过点P作PC⊥x轴,垂足为C点,直线AC交椭圆E与另一点B,当$k=\sqrt{2}$时,椭圆E的右焦点到直线l的距离为$\sqrt{2}$.
如图所示,已知椭圆$E:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$过点$({\sqrt{2},\sqrt{2}})$,直线l:y=kx(k≠0)与椭圆E交于P、A两点,过点P作PC⊥x轴,垂足为C点,直线AC交椭圆E与另一点B,当$k=\sqrt{2}$时,椭圆E的右焦点到直线l的距离为$\sqrt{2}$.