题目内容
1.已知f(x)=$\sqrt{3}$cos2x+2sin($\frac{3π}{2}$+x)sin(π-x),x∈R(1)求函数f(x)的单调递增区间
(2)已知锐角△ABC的内角A,B,C的对边分别为a,b,c,且f(A)=-$\sqrt{3}$,a=3,求△ABC面积的最大值.
分析 (1)利用诱导公式倍角公式与和差公式可得:f(x)=-2sin$(2x-\frac{π}{3})$,再利用正弦函数的单调性即可得出.
(2)f(A)=-$\sqrt{3}$,可得sin$(2A-\frac{π}{3})$=$\frac{\sqrt{3}}{2}$,$0<A<\frac{π}{2}$,解得A=$\frac{π}{3}$.再利用余弦定理与基本不等式的性质即可得出.
解答 解:(1)f(x)=$\sqrt{3}$cos2x+2sin($\frac{3π}{2}$+x)sin(π-x)
=$\sqrt{3}$cos2x-2cosxsinx=$\sqrt{3}$cos2x-sin2x=-2sin$(2x-\frac{π}{3})$,
由$\frac{π}{2}$+2kπ≤2x-$\frac{π}{3}$≤$\frac{3π}{2}$+2kπ,解得kπ+$\frac{5π}{12}$≤x≤$\frac{11π}{12}$+kπ,
因此函数f(x)的单调递增区间为:[kπ+$\frac{5π}{12}$,$\frac{11π}{12}$+kπ],k∈Z.
(2)f(A)=-$\sqrt{3}$,可得sin$(2A-\frac{π}{3})$=$\frac{\sqrt{3}}{2}$,∵$0<A<\frac{π}{2}$,∴$(2A-\frac{π}{3})$∈$(-\frac{π}{3},\frac{2π}{3})$,∴$2A-\frac{π}{3}$=$\frac{π}{3}$.
解得A=$\frac{π}{3}$.
由余弦定理可得:${3}^{2}={b}^{2}+{c}^{2}-2bccos\frac{π}{3}$≥2bc-bc=bc,可得bc≤9,当且仅当b=c=3时取等号.
∴S△ABC=$\frac{1}{2}bc$sinA≤$\frac{9\sqrt{3}}{4}$.
∴当且仅当a=b=c=3时,△ABC面积取得最大值$\frac{9\sqrt{3}}{4}$.
点评 本题考查了三角函数的图象与性质、诱导公式倍角公式与和差公式、余弦定理、三角形面积计算公式、基本不等式的性质,考查了推理能力与计算能力,属于中档题.

| A. | $\sqrt{3}$ | B. | 2 | C. | $2\sqrt{2}$ | D. | 4 |
| A. | [1,4] | B. | [2,6] | C. | [3,7] | D. | $[2\sqrt{2},4\sqrt{2}]$ |
”发生的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{2-\sqrt{2}}{2}$ | C. | $\frac{3-\sqrt{3}}{3}$ | D. | $\frac{2-\sqrt{3}}{2}$ |
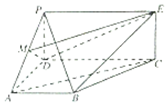 如图所示的几何体中,四边形PDCE为矩形,ABCD为直角梯形,且∠BAD=∠ADC=90°,平面PDCE⊥平面ABCD,AB=AD=$\frac{1}{2}$CD=1,PD=$\sqrt{2}$.
如图所示的几何体中,四边形PDCE为矩形,ABCD为直角梯形,且∠BAD=∠ADC=90°,平面PDCE⊥平面ABCD,AB=AD=$\frac{1}{2}$CD=1,PD=$\sqrt{2}$.