题目内容
4．一个袋中装有质地均匀，大小相同的2个黑球和3个白球，从袋中一次任意摸出2个球，则恰有1个是白球的概率为$\frac{3}{5}$，从袋中一次任意摸出3个球，摸出白球个数的数学期望Eξ是1.8．分析 从袋中一次任意摸出2个球，基本事件总数n=${C}_{5}^{2}$=10，恰有1个是白球包含的基本事件个数m=${C}_{2}^{1}{C}_{3}^{1}$=6，由此能示出恰有1个是白球的概率；从袋中一次任意摸出3个球，摸出白球个数ξ的可能取值为1，2，3，分别求出相应的概率，由此能求出数学期望Eξ．
解答 解：一个袋中装有质地均匀，大小相同的2个黑球和3个白球，
从袋中一次任意摸出2个球，
基本事件总数n=${C}_{5}^{2}$=10，
恰有1个是白球包含的基本事件个数m=${C}_{2}^{1}{C}_{3}^{1}$=6，
∴恰有1个是白球的概率为p=$\frac{m}{n}=\frac{6}{10}$=$\frac{3}{5}$．
从袋中一次任意摸出3个球，摸出白球个数ξ的可能取值为1，2，3，
P（ξ=1）=$\frac{{C}_{2}^{2}{C}_{3}^{1}}{{C}_{5}^{3}}$=$\frac{3}{10}$，
P（ξ=2）=$\frac{{C}_{2}^{1}{C}_{3}^{2}}{{C}_{5}^{3}}$=$\frac{6}{10}$，
P（ξ=3）=$\frac{{C}_{3}^{3}}{{C}_{5}^{3}}$=$\frac{1}{10}$，
∴数学期望Eξ=1×$\frac{3}{10}+2×\frac{6}{10}+3×\frac{1}{10}$=1.8．
故答案为：$\frac{3}{5}$，1.8．
点评 本题考查概率的求法，考查离散型随机变量的分布列及数学期望的求法，是中档题，在历年高考中都是必考题型之一．
练习册系列答案
相关题目
14．若函数y=2-|x|-k有零点，则实数k的取值范围是（ ）
| A． | k∈[-1，0） | B． | k∈[0，1] | C． | k∈（0，1] | D． | k∈[0，+∞） |
19．过双曲线x2-$\frac{{y}^{2}}{{b}^{2}}$=1（b＞0）的右焦点F作双曲线的一条渐近线的垂线，垂足为E，O为坐标原点，若∠OFE=2∠EOF，则b=（ ）
| A． | $\frac{1}{2}$ | B． | $\sqrt{3}$ | C． | 2 | D． | $\frac{\sqrt{3}}{3}$ |
9．已知$\overrightarrow a=（3，-4）$，$\overrightarrow b=（cosα，sinα）$，则$|{\overrightarrow a+2\overrightarrow b}|$的取值范围是（ ）
| A． | [1，4] | B． | [2，6] | C． | [3，7] | D． | $[2\sqrt{2}，4\sqrt{2}]$ |
16．已知圆C：x2+y2=1，直线l：y=k（x+2），在[-1，1]上随机选取一个数k，则事件“直线l与圆C相离
”发生的概率为（ ）
”发生的概率为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{2-\sqrt{2}}{2}$ | C． | $\frac{3-\sqrt{3}}{3}$ | D． | $\frac{2-\sqrt{3}}{2}$ |
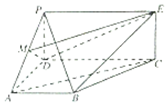如图所示的几何体中，四边形PDCE为矩形，ABCD为直角梯形，且∠BAD=∠ADC=90°，平面PDCE⊥平面ABCD，AB=AD=$\frac{1}{2}$CD=1，PD=$\sqrt{2}$．