题目内容
20.已知全集U=R,集合A={x|log2(x-2)<2},∁UB=(-∞,1)∪[4,+∞),则A∩B=( )| A. | (4,6] | B. | [1,6) | C. | (2,4] | D. | (2,4) |
分析 先根据对数函数的性质求出集合A,由全集U=R及B的补集确定出B,找出A与B的交集即可.
解答 解:∵A={x|log2(x-2)<2}=(2,6),
全集U=R,∁UB=(-∞,1)∪[4,+∞),
∴B=[1,4),
∴A∩B=(2,4),
故选:D.
点评 此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.一个几何体的三视图如图所示,则此几何体的体积为( )
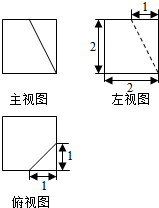

| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{23}{3}$ | D. | $\frac{22}{3}$ |
15.已知函数$f(x)=\left\{\begin{array}{l}{x^2}+2x,x∈(-∞,0)\\ ln(x+1),x∈[0,+∞).\end{array}\right.g(x)={x^2}-4x-4$,若存在实数a,使得f(a)+g(x)=0,则x的取值范围为( )
| A. | [-1,5] | B. | (-∞,-1]∪[5,+∞) | C. | [-1,+∞) | D. | (-∞,5] |
5.设a=e0.3,b=0.92,c=ln0.9,则a,b,c的大小关系是( )
| A. | a<b<c | B. | c<b<a | C. | c<a<b | D. | b<c<a |
12.已知a>0,函数f(x)=$\frac{|x-2a|}{x+2a}$在区间[1,4]上的最大值等于$\frac{1}{2}$,则a的值为( )
| A. | $\frac{2}{3}$或$\frac{3}{2}$ | B. | $\frac{3}{2}$ | C. | 2 | D. | $\frac{3}{2}$或2 |
9.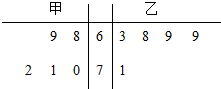 甲、乙两名同学五次数学测试的成绩统计用茎叶图表示(如图),则下列说法中正确的个数是( )
甲、乙两名同学五次数学测试的成绩统计用茎叶图表示(如图),则下列说法中正确的个数是( )
①甲的平均成绩比乙的平均成绩高;
②乙的成绩比甲的成绩稳定;
③甲的成绩极差比乙的成绩极差大;
④甲的中位数比乙的中位数大.
 甲、乙两名同学五次数学测试的成绩统计用茎叶图表示(如图),则下列说法中正确的个数是( )
甲、乙两名同学五次数学测试的成绩统计用茎叶图表示(如图),则下列说法中正确的个数是( )①甲的平均成绩比乙的平均成绩高;
②乙的成绩比甲的成绩稳定;
③甲的成绩极差比乙的成绩极差大;
④甲的中位数比乙的中位数大.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
10.三个数0.60.7,0.70.6,log0.76的大小顺序是( )
| A. | 0.60.7<0.70.6<log0.76 | B. | 0.60.7<log0.76<0.70.6 | ||
| C. | log0.76<0.60.7<0.70.6 | D. | log0.76<0.70.6<0.60.7 |
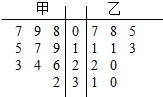 某赛季,甲、乙两名篮球运动员都参加了10场比赛,他们每场比赛得分的情况用如图所示的茎叶图表示,若甲运动员的中位数为a,乙运动员的众数为b,则a-b的值是( )
某赛季,甲、乙两名篮球运动员都参加了10场比赛,他们每场比赛得分的情况用如图所示的茎叶图表示,若甲运动员的中位数为a,乙运动员的众数为b,则a-b的值是( )