题目内容
13.函数y=asin(ax+θ)(a>0,θ≠0)图象上的一个最高点和其相邻最低点的距离的最小值为2$\sqrt{π}$.分析 根据题意画出图形,结合图形利用勾股定理即可求出图象上的一个最高点和其相邻最低点的距离的最小值.
解答 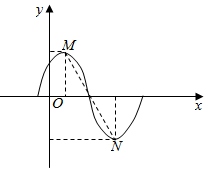 解:如图所示
解:如图所示
函数y=asin(ax+θ)(a>0,θ≠0)图象上的一个最高点M
和其相邻最低点N的距离的最小值为:
|MN|=$\sqrt{{(2a)}^{2}{+(\frac{π}{a})}^{2}}$=$\sqrt{{4a}^{2}+\frac{{π}^{2}}{{a}^{2}}}$≥$\sqrt{2\sqrt{{4a}^{2}•\frac{{π}^{2}}{{a}^{2}}}}$=2$\sqrt{π}$,
当且仅当4a2=$\frac{{π}^{2}}{{a}^{2}}$,即a=$\frac{π}{2}$时取“=”.
故答案为:2$\sqrt{π}$.
点评 本题考查了函数y=Asin(ωx+φ)的图象与性质的应用问题,是基础题目.

练习册系列答案
相关题目
3.设全集U=R,集合A={x|7-6x≤0},集合B={x|y=lg(x+2)},则(∁UA)∩B等于( )
| A. | (-2,$\frac{7}{6}$) | B. | ($\frac{7}{6}$,+∞) | C. | [-2,$\frac{7}{6}$) | D. | (-2,-$\frac{7}{6}$) |
1.在等比数列{an}中,a1=8,a4=64,则a3等于( )
| A. | 16 | B. | 16或-16 | C. | 32 | D. | 32或-32 |
5.下列函数中,在其定义域内是奇函数且是增函数的是( )
| A. | y=2x | B. | y=2|x| | C. | y=2-x-2x | D. | y=2x-2-x |
2.下面四个函数中,以π为最小正周期,且在区间($\frac{π}{2}$,π)上为减函数的是( )
| A. | y=cos2x | B. | y=2|sinx| | C. | y=($\frac{1}{3}$)cosx | D. | y=tanx |
 某校对高二年级进行了一次学业水平模块测试,从该年级学生中随机抽取部分学生,将他们的数学测试成绩分为6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100)加以统计,得到如图所示的频率分布直方图.已知高二年级共有学生600名,若成绩不少于80分的为优秀,据此估计,高二年级在这次测试中数学成绩优秀的学生人数为( )
某校对高二年级进行了一次学业水平模块测试,从该年级学生中随机抽取部分学生,将他们的数学测试成绩分为6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100)加以统计,得到如图所示的频率分布直方图.已知高二年级共有学生600名,若成绩不少于80分的为优秀,据此估计,高二年级在这次测试中数学成绩优秀的学生人数为( )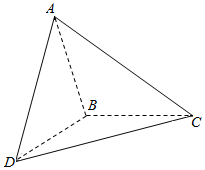 三棱锥A-BCD中,平面ABC⊥平面BCD,AB=BC=BD,∠ABC=∠DBC=120°,则二面角A-BD-C的平面角的正切值是-2.
三棱锥A-BCD中,平面ABC⊥平面BCD,AB=BC=BD,∠ABC=∠DBC=120°,则二面角A-BD-C的平面角的正切值是-2.