题目内容

1．在等比数列{an}中，a1=8，a4=64，则a3等于（　　）
A．16B．16或-16C．32D．32或-32

分析 设等比数列{an}的公比为q，根据题意分析可得q3=$\frac{64}{8}$=8，即q=2；进而由等比数列通项公式计算可得答案．

解答 解：根据题意，设等比数列{an}的公比为q，
又有a1=8，a4=64，
则q3=$\frac{64}{8}$=8，即q=2；
则a3=a1q2=8×22=32；
故选：C．

点评 本题考查等比数列的通项公式，关键是求出该数列的公比．

练习册系列答案
相关题目
11．设复数z满足（3-4i）z=|4+3i|（i是虚数单位），则复数z的虚部是（　　）
A．4B．4iC．$\frac{4}{5}$iD．$\frac{4}{5}$
12．若AB是圆x2+（y-3）2=1的任意一条直径，O为坐标原点，则$\overrightarrow{OA}•\overrightarrow{OB}$=8．
9．如图1，梯形ABCD中，AD⊥DC，AD∥BC，点E在线段AD上，AE=AB=BC=2，∠A=60°，现将三角形ABE沿BE折起，如图2，记$\overrightarrow{BA}$•$\overrightarrow{BC}$=λ
（1）当λ=1时，求证：平面ABE⊥平面BCDE；
（2）当λ=2时，求二面角A-CD-B的余弦值．
16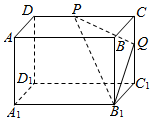．在长方体ABCD-A1B1C1D1中，AB=BC=$\sqrt{2}$AA1，P、Q分别是棱CD、CC1上的动点，如图．当BQ+QD1的长度取得最小值时，二面角B1-PQ-D1的余弦值的取值范围为（　　）
A．[0，$\frac{1}{5}$]B．[0，$\frac{\sqrt{10}}{10}$]C．[$\frac{1}{5}$，$\frac{\sqrt{10}}{10}$]D．[$\frac{\sqrt{10}}{10}$，1]
6．设U=R，已知集合A={x|x≥1}，B={x|x＞a}，且（∁UA）∪B=R，则实数a的取值范围是（　　）
A．（-∞，1）B．（-∞，1]C．（1，+∞）D．[1，+∞）
13．函数y=asin（ax+θ）（a＞0，θ≠0）图象上的一个最高点和其相邻最低点的距离的最小值为2$\sqrt{π}$．
10．已知复数z=i（1-i），则|z|=（　　）
A．2B．$\sqrt{2}$C．5D．$\sqrt{5}$
11．已知等比数列{an}满足an+1+an=10•4n-1（n∈N*），数列{bn}的前n项和为Sn，且bn=log2an．
（I）求bn，Sn；
（Ⅱ）设cn=$\frac{{b}_{n}+1}{2}$，证明：$\sqrt{{c}_{1}•{c}_{2}}$+${\sqrt{{c}_{2•}c}}_{3}$+…+${\sqrt{{c}_{n}•c}}_{n+1}$＜$\frac{1}{2}$Sn+1（n∈N*）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网