题目内容
1.已知圆的一般方程为x2+y2-2x+4y+3=0,则圆心C的坐标与半径分别是( )| A. | (1,-2),r=2 | B. | (1,-2),$r=\sqrt{2}$ | C. | (-1,2),r=2 | D. | (-1,2),$r=\sqrt{2}$ |
分析 利用配方法化圆的一般方程为标准方程,从而求得圆的圆心坐标和半径.
解答 解:由x2+y2-2x+4y+3=0,配方得(x-1)2+(y+2)2=2.
∴圆的圆心坐标为C(1,-2),半径为$\sqrt{2}$,
故选:B.
点评 本题考查圆的一般方程化标准方程,考查配方法,是基础题.

练习册系列答案
相关题目
13.下列函数为奇函数的是( )
| A. | $y={x^{\frac{1}{2}}}$ | B. | y=x-1 | C. | y=x2 | D. | y=x3 |
10.下面表格是两种教学实验的成绩对比统计,试分析两种教法的效果.
| 及格 | 不及格 | 合计 | |
| 掌握教学法 | 36 | 8 | 44 |
| 常规教学法 | 40 | 16 | 56 |
| 合计 | 76 | 24 | 100 |
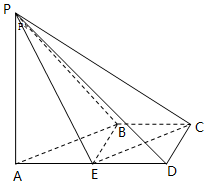 如图,在四棱锥P-ABCD中,AD∥BC,∠ADC=∠PAB=90°,BC=CD=$\frac{1}{2}$AD=1,E为棱AD的中点,异面直线PA与CD所成的角为90°.
如图,在四棱锥P-ABCD中,AD∥BC,∠ADC=∠PAB=90°,BC=CD=$\frac{1}{2}$AD=1,E为棱AD的中点,异面直线PA与CD所成的角为90°.