题目内容
1.下列命题正确的是( )| A. | 若两条直线和同一个平面所成的角相等,则这两条直线平行 | |
| B. | 若一个平面内有无数个点到另一个平面的距离相等,则这两个平面平行 | |
| C. | 若一条直线平行于两个相交平面的交线,则这条直线与这两个平面都平行 | |
| D. | 若两个平面都垂直于第三个平面,则这两个平面平行或相交 |
分析 作出正方体,对ABCD四个选项逐一结合图形分析即可得到答案.
解答 解:作图如下: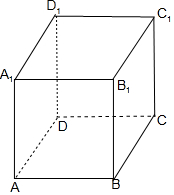
A.若两条直线和同一个平面所成的角相等,则这两条直线相交(如相交直线A1D1与A1B1与底面ABCD均成0°角)、平行(如A1D1与B1C1与底面ABCD均成0°角,但A1D1∥B1C1)或异面(AD1与B1C均与底面ABCD成45°角,但二者为异面直线),故A错误;
B.若一个平面内有无数个点到另一个平面的距离相等,则这两个平面平行(如图中上下两个底面)或相交(平面DCC1DI上有无数个点到平面ABCD的距离相等,但平面DCC1DI与底面ABCD相交),故B错误;
C.若一条直线平行于两个相交平面的交线,则这条直线与这两个平面都平行(如平面DCC1DI∩平面ABCD=CD,A1B1∥CD,且A1B1∥平面DCC1DI,A1B1∥平面ABCD)或这条直线在其中一平面内(如平面DCC1DI∩平面ABCD=CD,C1D1∥CD,但C1D1?平面DCC1DI,故C错误;
D.若两个平面都垂直于第三个平面,则这两个平面平行(如图中上下两个底面平行,均与平面A1ABB1垂直)或相交(如图中平面ADD1A1与平面DCC1D1均与底面垂直,但二者相交),故D正确.
故选:D.
点评 本题考查空间中直线与直线、直线与平面、平面与平面的位置关系,考查空间想象能力,属于中档题.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
9.以下是某地搜集到的新房屋的销售价格y与房屋的面积x的数据:
数据对应的散点图如图所示;
(1)求线性回归方程.(参考公式:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$)
(参考数据 $\overline{x}$=$\frac{1}{5}$$\sum_{i=1}^{5}$xi=109,$\sum_{i=1}^{5}$(xi-$\overline{x}$)2=1570,$\sum_{i=1}^{5}$(xi-$\overline{x}$)(yi-$\overline{y}$)=311.2)
(2)据(1)的结果估计当房屋面积为150m2时的销售价格.
| 房屋面积(m2) | 115 | 110 | 80 | 135 | 105 |
| 销售价格(万元) | 24.8 | 21.6 | 18.4 | 29.2 | 22 |
(1)求线性回归方程.(参考公式:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$)
(参考数据 $\overline{x}$=$\frac{1}{5}$$\sum_{i=1}^{5}$xi=109,$\sum_{i=1}^{5}$(xi-$\overline{x}$)2=1570,$\sum_{i=1}^{5}$(xi-$\overline{x}$)(yi-$\overline{y}$)=311.2)
(2)据(1)的结果估计当房屋面积为150m2时的销售价格.
6.已知四面体ABCD的六条棱中,AC=BD=4,其余的四条棱的长都是3,则此四面体的外接球的表面积为( )
| A. | 43π | B. | 17π | C. | 34π | D. | $\frac{17π}{3}$ |
13.若x为三角形中的最小内角,则函数y=$\sqrt{2}sin({x+{{45}°}})$的值域是( )
| A. | $(0,\frac{{\sqrt{2}}}{2}]$ | B. | $[\frac{1}{2},\frac{{\sqrt{2}}}{2}]$ | C. | $(\frac{1}{2},\frac{{\sqrt{2}}}{2}]$ | D. | $(1,\sqrt{2}]$ |
11.正方体的表面积是64,则正方体的体对角线的长为( )
| A. | 4$\sqrt{3}$ | B. | 3$\sqrt{4}$ | C. | 4$\sqrt{2}$ | D. | 16 |