Question

【题目】将正方形沿对角线折成直二面角，

①与平面所成角的大小为

②是等边三角形

③与所成的角为

④

⑤二面角为

则上面结论正确的为_______．

Answer 1

【答案】②③④

【解析】

作出此直二面角的图象，由图形中所给的位置关系对命题逐一判断，即可得出正确结论．

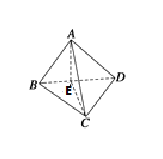
作出如图的图象，E是BD的中点，易得∠AED＝90°即为此直二面角的平面角

对于命题①AB与平面BCD所成的线面角的平面角是∠ABE＝45°，故AB与平面BCD成60°的角不正确；

对于命题②，在等腰直角三角形AEC中AC等于正方形的边长，故△ACD是等边三角形，此命题正确；

对于命题③可取AD中点F，AC的中点H，连接EF，EH，FH，则EF，FH是中位线，故∠EFH或其补角为异面直线AB与CD所成角，又EF,FH其长度为正方形边长的一半，而EH是直角三角形AEC的中线，其长度是AC的一半即正方形边长的一半，故△EFH是等边三角形，由此AB与CD所成的角为60°，此命题正确；

对于命题④，BD⊥面AEC，故AC⊥BD，此命题正确；

对于命题⑤，连接BH，HD,则BH⊥AC, DH⊥AC,则∠BHD为二面角的平面角，又BH=DH=AC,BD=∠BHD=-故二面角不是

综上知②③④是正确的

故答案为②③④